6．如图，点P在边长为1的正方形ABCD上运动，设点M为CD的中点，当点P沿A→B→C→M运动时，点P经过的路程设为x，△APM的面积设为y，则函数y＝f(x)的图象只可能是下图中的(　)

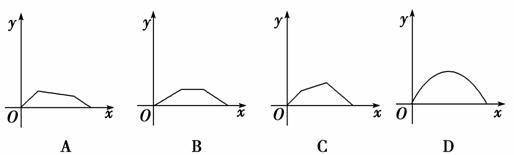
解析：选A.据题意可得f(x)＝易知只有A选项符合条件．

5．已知函数f(x)＝ax²－x－c，且f(x)＞0的解集为(－2,1)，则函数y＝f(－x)的图象为(　)

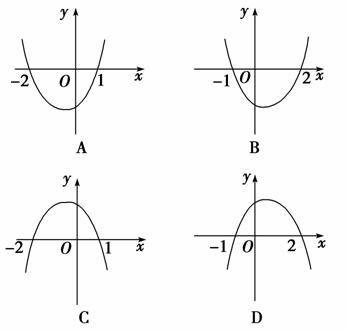
解析：选D.由ax²－x－c＞0的解集为(－2,1)，

得∴

∴f(x)＝－x²－x+2.

∴f(－x)＝－x²+x+2，图象为D.

4．下列各组函数是同一函数的是(　)

A．y＝与y＝1

B．y＝|x－1|与y＝

C．y＝|x|+|x－1|与y＝2x－1

D．y＝与y＝x

解析：选D.∵y＝＝，定义域与对应法则都不同，∴排除A.

又∵y＝|x－1|＝，定义域不同，∴排除B.

y＝|x|+|x－1|＝，对应法则不同，∴排除C.

y＝＝＝x，故选D.

3．(2010年北京西城模拟)设f：x→x²是集合A到集合B的映射，如果B＝{1,2}，则A∩B等于(　)

A．{1}　 　　　　　　　　　B．∅

C．∅或{1}　 　　　　　　　　D．∅或{2}

解析：选C.由已知可得集合A是集合{－，－1,1，}的非空子集，则A∩B＝∅或{1}．

2．设函数f(x)＝，则f(f(f()－5))＝(　)

A．3 　　　　　　　　　　　B．4

C．7　 　　　　　　　　　　D．9

解析：选C.本题在求解时要注意自变量的取值范围与相对应的解析式，f(f(f()－5))＝f(f(－1))＝f(－3)＝7.

1．设A＝{x|0≤x≤2}，B＝{y|1≤y≤2}，在下列各图中能表示从集合A到集合B的映射的是(　)

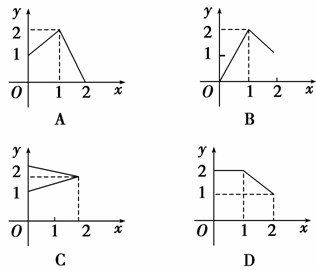
解析：选D.A中的元素在B中都有唯一元素相对应．

6．(1)已知f(x－2)＝3x－5，求f(x)；

(2)已知f(1－cosx)＝sin²x，求f(x)；

(3)若f{f[f(x)]}＝27x+26，求一次函数f(x)的解析式．

解：(1)令t＝x－2，则x＝t+2，t∈R，

由已知有：f(t)＝3(t+2)－5＝3t+1，

故f(x)＝3x+1.

(2)∵f(1－cosx)＝sin²x＝1－cos²x，

令1－cosx＝t，cosx＝1－t，

∵－1≤cosx≤1，

∴0≤1－cosx≤2，∴0≤t≤2，

∴f(t)＝1－(1－t)²＝－t²+2t(0≤t≤2)，

故f(x)＝－x²+2x(0≤x≤2)．

(3)设f(x)＝ax+b(a≠0)，f[f(x)]＝a²x+ab+b，

f{f[f(x)]}＝a(a²x+ab+b)+b＝a³x+a²b+ab+b，

∴

解得a＝3，b＝2.

则f(x)＝3x+2，f[f(x)]＝3(3x+2)+2＝9x+8.

f{f[f(x)]}＝3(9x+8)+2＝27x+26，

∴a＝3，b＝2，f(x)＝3x+2为所求．

练习

5．若f(x)＝x²+bx+c，且f(1)＝0，f(3)＝0，则f(－1)＝________.

解析：依题意有，

解得，

∴f(x)＝x²－4x+3，

∴f(－1)＝(－1)²－4×(－1)+3＝8.

答案：8

4．若f(x－1)＝2x+5，则f(x²)＝________.

解析：令x－1＝t，则x＝t+1，f(t)＝2(t+1)+5＝2t+7，

∴f(x²)＝2x²+7.

答案：2x²+7

3．(2010年佛山质检)已知函数f(x)＝，若f[f(x)]＝2，则x的取值范围是(　)

A．∅ 　　　　　　　　　　　　B．[－1,1]

C．(－∞，－1)∪(1，+∞)　 　D．{2}∪[－1,1]

解析：选D.若x∈[－1,1]，则有f(x)＝2∉[－1,1]，∴f(2)＝2；若x∉[－1,1]，则f(x)＝x∉[－1,1]，∴f[f(x)]＝x，此时若f[f(x)]＝2，则有x＝2.