8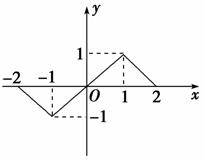．函数y＝f(x)(x∈[－2,2])的图象如图所示，则f(x)+f(－x)＝________.

解析：由图象可知f(x)为定义域上的奇函数．

∴f(x)+f(－x)＝f(x)－f(x)＝0.

答案：0

7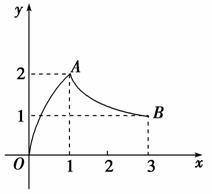．如图，函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0,0)，(1,2)，(3,1)，则f()的值等于________．

解析：∵f(3)＝1，∴＝1，

∴f()＝f(1)＝2.

答案：2

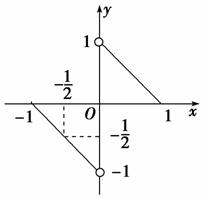
6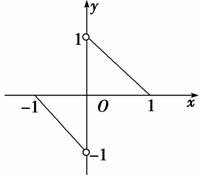．函数f(x)的图象是两条直线的一部分(如图所示)，其定义域为[－1,0)∪(0,1]，则不等式f(x)－f(－x)＞－1的解集是(　)

A．{x|－1≤x≤1且x≠0}

B．{x|－1≤x＜0}

C．{x|－1≤x＜0或＜x≤1}

D．{x|－1≤x＜－或0＜x≤1}

解析：选D.由图可知，f(x)为奇函数．

∴f(－x)＝－f(x)，

∴f(x)－f(－x)＞－1

⇔2f(x)＞－1

⇔f(x)＞－⇔－1≤x＜－或0＜x≤1.故选D.

5.下列函数的图象，经过平移或翻折后不能与函数y＝log₂x的图象重合的函数是(　)

A．y＝2^x　　　　B．y＝logx

C．y＝·4^x 　　　　　　D．y＝log₂+1

解析：选C.y＝log₂x与y＝2^x关于y＝x对称；y＝log₂x与y＝logx关于x轴对称；而y＝log₂+1的图象可由y＝log₂x的图象翻折再平移得到．

4．(2009年高考北京卷)为了得到函数y＝lg的图象，只需把函数y＝lgx的图象上所有的点(　)

A．向左平移3个单位长度，再向上平移1个单位长度

B．向右平移3个单位长度，再向上平移1个单位长度

C．向左平移3个单位长度，再向下平移1个单位长度

D．向右平移3个单位长度，再向下平移1个单位长度

解析：选C.∵y＝lg＝lg(x+3)－1，∴将y＝lgx的图象上的点向左平移3个单位长度得到y＝lg(x+3)的图象，再将y＝lg(x+3)的图象上的点向下平移1个单位长度得到y＝lg(x+3)－1的图象．

3．函数y＝f(x)的图象如图所示，则函数y＝log_0.5f(x)的图象大致是(　)

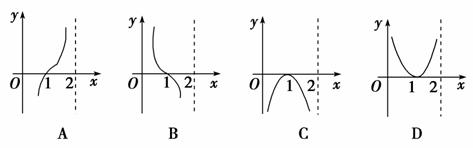
解析：选C.由同增异减的单调性原则可得：当x∈(0,1)时y＝log_0.5f(x)为增函数，且y＜0，当x∈(1,2)时y＝log_0.5f(x)为减函数，且－1＜y＜0，分析各选项易知只有C符合上述条件．

2．(2009年高考安徽卷)设a＜b，函数y＝(x－a)²(x－b)的图象可能是(　)

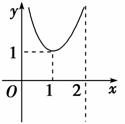解析：选C.当x＞b时，y＞0，x＜b时，y≤0.故选C.

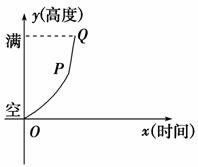
1．有一空容器，由悬在它上方的一根水管均匀地注水，直至把容器注满，在注水过程中水面的高度变化曲线如图所示，其中PQ为一线段，则与此图相对应的容器的形状是(　)

解析：选C.由函数图象可判断出该容器必定有不规则形状，再由PQ为直线段，容器上端必是直的一段，故可排除ABD，选C.

6．(1)作函数y＝|x－x²|的图象；

(2)作函数y＝x²－|x|的图象．

解：(1)y＝

即y＝其图象如图①所示．

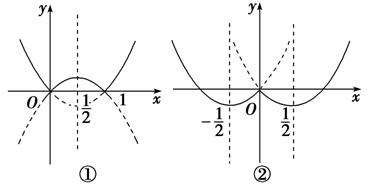
(2)y＝

即y＝其图象如图②所示．

练习

5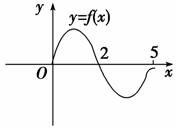．设奇函数f(x)的定义域为[－5,5]，若当x∈[0,5]时，f(x)的图象如图，则不等式f(x)＜0的解集是________．

解析：由奇函数图象的特征可得f(x)在 [－5,5]上的图象．由图象可解出结果．

答案：{x|－2＜x＜0或2＜x≤5}