6.已知函数f(x)＝－(a＞0，x＞0)．

(1)求证：f(x)在(0，+∞)上是增函数；

(2)若f(x)在[，2]上的值域是[，2]，求a的值．

解：(1)证明：设x₂＞x₁＞0，

则x₂－x₁＞0，x₁x₂＞0.

∵f(x₂)－f(x₁)＝(－)－(－)

＝－＝＞0，

∴f(x₂)＞f(x₁)，∴f(x)在(0，+∞)上是增函数．

(2)∵f(x)在[，2]上的值域是[，2]，

又f(x)在[，2]上单调递增，

∴f()＝，f(2)＝2，代入可得a＝.

练习

5．(2008年高考上海卷)若函数f(x)＝(x+a)(bx+2a)(常数a、b∈R)是偶函数，且它的值域为(－∞，4]，则该函数的解析式f(x)＝________________.

解析：由于f(x)的定义域为R，值域为(－∞，4]，

可知b≠0，∴f(x)为二次函数，

f(x)＝(x+a)(bx+2a)

＝bx²+(2a+ab)x+2a².

∵f(x)为偶函数，

∴其对称轴为x＝0，∴－＝0，

∴2a+ab＝0，∴a＝0或b＝－2.

若a＝0，则f(x)＝bx²与值域是(－∞，4]矛盾，∴a≠0，

若b＝－2，又其最大值为4，

∴＝4，∴2a²＝4，

∴f(x)＝－2x²+4.

答案：－2x²+4

4．(原创题)已知f(x)＝x²+x，则f(a+)________f(1)．(填“≤”“≥”)．

解析：∵a+≥2或a+≤－2，

f(x)的对称轴为x＝－.

∴f(x)在(－，+∞)上为增函数，

在(－∞，－)上为减函数．

又f(2)＝2²+2＝6>2＝f(1)，

f(－2)＝(－2)²+(－2)＝2＝f(1)，

∴f(a+)≥f(1)．

答案：≥

3．已知函数f(x)为R上的减函数，则满足f(||)＜f(1)的实数x的取值范围是(　)

A．(－1,1)　 　　　　　　　　　B．(0,1)

C．(－1,0)∪(0,1)　　　　　 　D．(－∞，－1)∪(1，+∞)

解析：选C.∵f(x)在R上为减函数且f(||)＜f(1)，

∴||＞1，

即|x|＜1且x≠0，得－1＜x＜0或0＜x＜1.

2．(2009年高考福建卷)下列函数f(x)中，满足“对任意的x₁，x₂∈(0，+∞)，当x₁＜x₂时，都有f(x₁)＞f(x₂)”的是(　)

A．f(x)＝　 　　　　　　　B．f(x)＝(x－1)²

C．f(x)＝e^x　 　　　　　　D．f(x)＝ln(x+1)

解析：选A.由题意知函数f(x)在(0，+∞)上是减函数，

在A中，由f′(x)＝－＜0得f(x)在(－∞，0)和(0，+∞)上为减函数；

在B中，由f′(x)＝2(x－1)＜0得x＜1，所以f(x)在(－∞，1)上为减函数．

在C中，由f′(x)＝e^x＞0知f(x)在R上为增函数．

在D中，由f′(x)＝且x+1＞0知f′(x)＞0，所以f(x)在(－1，+∞)上为减函数．

1．(2010年皖南八校联考)设函数f(x)是定义在R上的奇函数，且f(－3)＝－2，则f(3)+f(0)＝(　)

A．3　　　　　B．－3

C．2 　　　　　　　　　　D．7

解析：选C.由题意得f(3)+f(0)＝－f(－3)+f(0)＝2+0＝2.故选C.

12．已知函数f(x)＝m(x+)的图象与h(x)＝(x+)+2的图象关于点A(0,1)对称．

(1)求m的值；

(2)若g(x)＝f(x)+在(0,2]上是减函数，求实数a的取值范围．

解：(1)设P(x，y)是h(x)图象上一点，点P关于A(0,1)的对称点为Q(x₀，y₀)，则x₀＝－x，y₀＝2－y.

∴2－y＝m(－x－)，

∴y＝m(x+)+2，从而m＝.

(2)g(x)＝(x+)+＝(x+)．

设0<x₁<x₂≤2，

则g(x₁)－g(x₂)＝(x₁+)－(x₂+)

＝(x₁－x₂)+(a+1)·

＝(x₁－x₂)·>0，

并且在x₁，x₂∈(0,2]上恒成立，

∴x₁x₂－(a+1)<0，∴1+a>x₁x_2,1+a≥4，∴a≥3.

11.若1＜x＜3，a为何值时，x²－5x+3+a＝0有两解、一解、无解？

解：原方程化为：a＝－x²+5x－3，①,作出函数y＝－x²+5x－3(1＜x＜3)的图象如图．

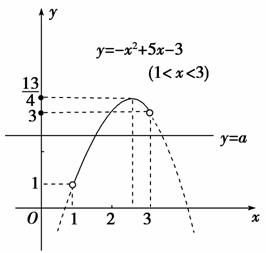
显然该图象与直线y＝a的交点的横坐标是方程①的解，由图可知：当3＜a＜时，原方程有两解；

当1＜a≤3或a＝时，原方程有一解；

当a＞或a≤1时，原方程无解．

10．已知函数f(x)＝

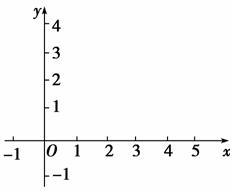
(1)在如图给定的直角坐标系内画出f(x)的图象；

(2)写出f(x)的单调递增区间．

解：(1)函数f(x)的图象如图所示．,

(2)由图象可知，函数f(x)的单调递增区间为[－1,0]，[2,5]．

9．已知函数f(x)＝2－x²，g(x)＝x.若f(x)*g(x)＝min{f(x)，g(x)}，那么f(x)*g(x)的最大值是________．(注意：min表示最小值)

解析：画出示意图

f(x)*g(x)＝

其最大值为1.

答案：1