3．函数y＝的定义域是(－∞，1)∪[2,5)，则其值域是(　)

A．(－∞，0)∪(，2]　 　　　　B．(－∞，2]

C．(－∞，)∪[2，+∞)　 　　　D．(0，+∞)

解析：选A.∵x∈(－∞，1)∪[2,5)，则x－1∈(－∞，0)∪[1,4)．∴∈(－∞，0)∪(，2]．故应选A.

2．函数y＝的定义域是(　)

A．{x|x＜0}　 　　　　　　　　B．{x|x＞0}

C．{x|x＜0且x≠－1}　 　　　　D．{x|x≠0且x≠－1，x∈R}

解析：选C.要使函数有意义，则，

解得x＜0且x≠－1.

1．(2008年高考全国卷Ⅰ)函数y＝+的定义域为(　)

A．{x|x≤1}　 　　　　　　　　B．{x|x≥0}

C．{x|x≥1或x≤0}　 　　　　　D．{x|0≤x≤1}

解析：选D.⇔0≤x≤1.

∴y＝+的定义域为{x|0≤x≤1}．

6．已知函数f(x)＝的定义域为R，试求实数m的取值范围．

解：由题意2^2x+m·2^x+1≠0对任意实数x都成立．

即m≠－(2^x+)在实数范围内恒成立．

令g(x)＝－(2^x+)，∵2^x＞0，

∴g(x)＝－(2^x+)≤－2＝－2，当且仅当x＝0时，“＝”成立．

故函数g(x)的值域是(－∞，－2]．

∴m的取值范围是m＞－2.

练习

5．(2008年高考安徽卷)函数f(x)＝的定义域为________．

解析：⇔

∴x≥3.

答案：{x|x≥3}

4．函数y＝的定义域为________．

解析：由题得lgx+1≥0，且x－1≠0，解得x≥，且x≠1，

∴x∈[，1)∪(1，+∞)．

答案：[，1)∪(1，+∞)

3．(2010年浙江金华十校模拟)已知函数f(x)＝log₂(3^x+－2)，则f(x)的值域为(　)

A．(－∞，－2)　 　　　　　B．(－2,2)

C．(－∞，+∞)　 　　　　　D．[0，+∞)

解析：选C.∵3^x＞0，∴3^x+≥2(x＝0时取“＝”)．令t＝3^x+－2，则t≥0，∴y＝log₂t(t＞0)的值域为R，选C.

2．若函数f(x)＝(a²－2a－3)x²+(a－3)x+1的定义域和值域都为R，则a的取值范围是(　)

A．a＝－1或a＝3　 　　　　B．a＝－1

C．a＝3　 　　　　　　　　　D．a不存在

解析：选B.依题意应有，解得a＝－1.

1．(原创题)已知函数f(x)＝lg(4－x)的定义域为M，g(x)＝的值域为N，则M∩N＝(　)

A．M　 　　　　　　　　　　B．N

C．[0,4)　 　　　　　　　　　D．[0，+∞)

解析：选C.M＝{x|x＜4}，N＝{y|y≥0}，∴M∩N＝[0,4)．

12．已知函数f(x)＝是奇函数．

(1)求实数m的值；

(2)若函数f(x)在区间[－1，a－2]上单调递增，求实数a的取值范围．

解：(1)设x＜0，则－x＞0，

所以f(－x)＝－(－x)²+2(－x)＝－x²－2x，

又f(x)为奇函数，所以f(－x)＝－f(x)，

于是x＜0时，f(x)＝x²+2x＝x²+mx，

所以m＝2.

(2)要使f(x)在[－1，a－2]上单调递增，

结合f(x)的图象知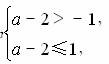

所以1＜a≤3，故实数a的取值范围是(1,3]．