1．袋中有红色、黄色、绿色球各一个，每次任取一个球，有放回地抽取三次，所取球的颜色全相同的概率是(　)

A.　 　　　　　　　　　　　B.

C.　 　　　　　　　　　　　D.

解析：选A.记“所取球的颜色全相同”为事件A，有放回地抽取三次共有27个等可能事件，事件A包含其中的3个基本事件，∴P(A)＝＝.故选A.

12．某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元．该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元．

(1)当一次订购量为多少个时，零件的实际出厂单价恰降为51元？

(2)设一次订购量为x个，零件的实际出厂单价为P元，写出函数P＝f(x)的表达式．

(3)当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利润又是多少元？(工厂售出一个零件的利润＝实际出厂单价－成本)

解：(1)设一次订购量为m个时，零件的实际出厂单价恰降为51元．

由题意，得60－(m－100)×0.02＝51，得m＝550.

故当一次订购550个时，零件实际出厂单价恰降为51元．

(2)由题意知，当0＜x≤100时，f(x)＝60；

当100＜x＜550时，f(x)＝60－(x－100)·0.02＝62－；

当x≥550时，f(x)＝51.

∴函数P＝f(x)的表达式是

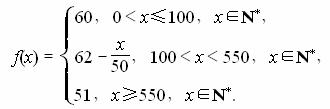
(3)由(2)知当销售商一次订购500个零件和1000个零件时销售单价分别为62－＝52(元)和51元，故其利润分别是500×52－500×40＝6000(元)和1000×51－1000×40＝11000(元)．

11．已知函数f(x)＝x²+2x+a，x∈[1，+∞)．

(1)当a＝时，求函数f(x)的最小值；

(2)若对任意x∈[1，+∞)，f(x)＞0恒成立，试求实数a的取值范围．

解：(1)a＝时，f(x)＝x²+2x+，

其图象是开口向上的抛物线，对称轴为x＝－1，

又∵x∈[1，+∞)，

∴f(x)的最小值是f(1)＝.

(2)由(1)知f(x)在[1，+∞)上的最小值是f(1)＝a+3.

∵f(x)＞0在[1，+∞)上恒成立，

故只需a+3＞0即可，解得a＞－3.

∴实数a的取值范围是a＞－3.

10．求下列函数的定义域和值域．

(1)y＝ － ；

(2)y＝log₂(x²－2x+1)；

(3)

解：(1)要使函数有意义，则

∴0≤x≤1，函数的定义域为[0,1]

∵函数y＝ － 为减函数，

∴函数的值域为[－1,1]．

(2)要使函数有意义，则x²－2x+1>0，∴x≠1，

函数的定义域为{x|x≠1，x∈R}．

∵x²－2x+1∈(0，+∞)，∴函数的值域为R.

(3)函数的定义域为{0,1,2,3,4,5}，

函数的值域为{2,3,4,5,6,7}．

9．(2010年石家庄模拟)函数f(x)＝log(x－1)+的值域为________．

解析：由，解得1＜x≤2，

∴函数f(x)的定义域为(1,2]．

又∵函数y₁＝log(x－1)和y₂＝在(1,2]上都是减函数，

∴当x＝2时，f(x)有最小值，

f(2)＝log(2－1)+＝0，

f(x)无最大值，∴函数f(x)的值域为[0，+∞)．

答案：[0，+∞)

8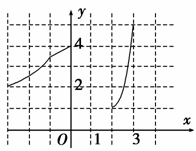．函数y＝f(x)的图象如图所示，那么，f(x)的定义域是______；值域是________；其中只与x的一个值对应的y值的范围是________．

解析：由图象知，函数y＝f(x)的图象包括两部分，一部分是以点(－3,2)和(0,4)为两个端点的一条曲线段，一部分是以(2,1)为起点到(3,5)结束的曲线段，故其定义域是[－3,0]∪[2,3]，值域为[1,5]，只与x的一个值对应的y值的取值范围是[1,2)∪(4,5]．

答案：[－3,0]∪[2,3]　[1,5]　[1,2)∪(4,5]

7．函数f(x)＝++lg(4－x)的定义域为________．

解析：由sinx≠0知x≠kπ，k∈Z，又

∴3≤x＜4，∴x∈[3，π)∪(π，4)．

答案：[3，π)∪(π，4)

6．(2008年高考江西卷)若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝的定义域是(　)

A．[0,1]　 　　　　　　　　　B．[0,1)

C．[0,1)∪(1,4] 　　　　　　D．(0,1)

解析：选B.∵y＝f(x)的定义域为[0,2]，

∴g(x)的定义域需满足，

解得0≤x＜1，故选B.

5.若函数y＝f(x)的值域是[，3]，则函数F(x)＝f(x)+的值域是(　)

A．[，3] 　　　　　　　　　B．[2，]

C．[，]　 　　　　　　　　D．[3，]

解析：选B.令f(x)＝t，t∈[，3]．问题转化为求函数y＝t+，t∈[，3]的值域．于是由函数y＝t+在[，1]上递减，在[1,3]上递增，得y∈[2，]．故选B.

4．下列函数中，值域是[－2,2]的是(　)

A．f(x)＝2^x－1　 　　　　　　　　B．f(x)＝log_0.5(x+11)

C．f(x)＝　 　　　　　　　　D．f(x)＝x²(4－x²)

解析：选C.A的值域为(0，+∞)；B的值域为R；C的值域为[－2,2]；D中有：f(x)＝－x⁴+4x²＝－(x²－2)²+4≤4，即值域为(－∞，4]．故选C.