4．若(x²+)ⁿ展开式的各项系数之和为32，则n＝________，其展开式中的常数项为________(用数字作答)．

解析：令x＝1，得2ⁿ＝32，得n＝5，

则T_r+1＝C₅^r·(x²)^5－r·()^r＝C₅^r·x^10－5r，

令10－5r＝0，r＝2.故常数项T₃＝10.

答案：5　10

3．(2010年沈阳高中质检)已知n为等差数列－4，－2,0，…中的第8项，则二项式(x²+)ⁿ展开式中常数项是(　)

A．第7项　 　　　　　　B．第8项

C．第9项　 　　　　　　D．第10项

解析：选C.由前几项可得通项为

a_m＝2m－6，a₈＝2×8－6＝10，

T_r+1＝C₁₀^rx^20－2r·2^rx－＝2^rC₁₀^rx20－r，

令20－r＝0，得r＝8.故为8+1＝9项，故选C.

2．(2008年高考安徽卷)设(1+x)⁸＝a₀+a₁x+…+a₈x⁸，则a₀，a₁，…，a₈中奇数的个数为(　)

A．2 　　　　　　　　　B．3

C．4　 　　　　　　　　　D．5

解析：选A.由(1+x)⁸＝a₀+a₁x+a₂x²+…+a₈x⁸可以知道，a₀、a₁、a₂、…、a₈均为二项式系数，依次是C₈⁰、C₈¹、C₈²、…、C₈⁸，

∵C₈⁰＝C₈⁸＝1，C₈¹＝C₈⁷＝8，C₈²＝C₈⁶＝28，C₈³＝C₈⁵＝56，

C₈⁴＝70，∴a₀，a₁，…，a₈中奇数只有a₀和a₈两个．

1．(2x－1)⁶的展开式中x²的系数为(　)

A．15 　　　　　　　　　B．60

C．120　 　　　　　　　　D．240

解析：选B.(2x－1)⁶＝(－1+2x)⁶⇒T₃＝C₆²(－1)⁴·(2x)²＝60x².选B.

5．不等式组所确定的平面区域记为D.点(x，y)是区域D上的点，若圆O：x²+y²＝r²上的所有点都在区域D上，则圆O的面积的最大值是________．

解析：画出不等式组所表示的平面区域(略)，其中离原点最近的距离为，故r的最大值为，所以圆O的面积的最大值是.

4．(2009年高考上海卷)已知实数x、y满足则目标函数z＝x－2y的最小值是________．

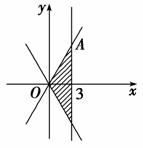解析：如图作出阴影部分为可行域，由得即A(3,6)，经过分析可知直线z＝x－2y经过A点时取最小值为－9.

答案：－9

3.已知实数x，y满足，如果目标函数z＝x－y的最小值为－1，则实数m等于(　)

A．7 　　　　　　　　B．5

C．4　 　　　　　　　D．3

解析：选B.将直线y＝x+1与y＝2x－1联立解得A(2,3)，据题意即为最优解，又点A必在直线x+y＝m上，代入求得m＝5.

2．(2009年高考福建卷)在平面直角坐标系中，若不等式组(a为常数)所表示的平面区域的面积等于2，则a的值为(　)

A．－5 　　　　　　　　　B．1

C．2　 　　　　　　　　　　D．3

解析：选D.由得A(1，a+1)，

由得B(1,0)，

由得C(0,1)．

∵△ABC的面积为2，且a>－1，

∴S_△ABC＝|a+1|＝2，∴a＝3.

1．已知(3,1)和(－4,6)在直线3x－2y+a＝0的两侧，则a的取值范围是(　)

A．a<1或a>24　 　　　　　B．a＝7或a＝24

C．－7<a<24　 　　　　　　D．－24<a<7

解析：选C.将点代入直线中，只要异号即可．

12．复数z₁＝+(10－a²)i，z₂＝+(2a－5)i，若₁+z₂是实数，求实数a的值．

解：₁+z₂＝+(a²－10)i++(2a－5)i

＝(+)+[(a²－10)+(2a－5)]i

＝+(a²+2a－15)i.

∵₁+z₂是实数，∴a²+2a－15＝0.解得a＝－5或a＝3.

∵分母a+5≠0，∴a≠－5，故a＝3.