
题目列表(包括答案和解析)
2.在2009年全运会女子百米冠军王静传出兴奋剂事件后,许多网民表达了自己的意见,有的网友进行了调查,在参加调查的4258名男性公民中有2360名认为其服用了兴奋剂,3890名女性公民中有2386人认为遭人陷害,在运用这些数据说明王静兴奋剂事件是否遭人陷害时用什么方法最有说服力? ( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
1.己知全集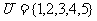 ,
,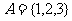 ,
,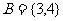 ,则
,则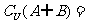 ( )
( )
(A)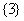 (B)
(B)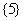 (C)
(C)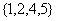 (D)
(D) 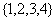
4.(原创题)设X-B(2,p),Y-B(4,p),已知P(X≥1)=,则P(Y≥1)=________.
解析:由1-C20p0(1-p)2=得p=,由1-C40()0()4=.
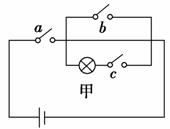
3.(2010年厦门市高中调研)如图所示的电路,有a,b,c三个开关,每个开关开或关的概率都是,且是相互独立的,则灯泡甲亮的概率为( )
A. B.
C. D.
解析:选A.理解事件之间的关系,设“a闭合”为事件A,“b闭合”为事件B,“c闭合”为事件C,则灯亮应为事件AC,且A,C,间彼此独立,
且P(A)=P()=P(C)=.
所以P(AC)=P(A)P()P(C)=.
2.(2008年高考福建卷)某一批花生种子,如果每1粒发芽的概率为,那么播下3粒种子恰有2粒发芽的概率是( )
A. B.
C. D.
解析:选C.由题意,3粒种子恰有2粒发芽,相当于3次独立试验有2次发生,
 故P(X=2)=C32·()2·(1-)=.
故P(X=2)=C32·()2·(1-)=.
1.(2009年高考上海卷)若事件E与F相互独立,且P(E)=P(F)=,则P(EF)的值等于( )
A.0 B.
C. D.
解析:选B.EF表示E与F同时发生,
∴P(EF)=P(E)·P(F)=.故选B.
12.已知f(x)=(1+x)m+(1+2x)n(m,n∈N*)的展开式中x的系数为11.
(1)求x2的系数取最小值时n的值.
(2)当x2的系数取得最小值时,求f(x)展开式中x的奇次幂项的系数之和.
解:(1)由已知Cm1+2Cn1=11,∴m+2n=11,
x2的系数为Cm2+22Cn2=+2n(n-1)
=+(11-m)(-1)
=(m-)2+.
∵m∈N*,∴m=5时,x2的系数取得最小值22,
此时n=3.
(2)由(1)知,当x2的系数取得最小值时,m=5,n=3,
∴f(x)=(1+x)5+(1+2x)3.
设这时f(x)的展开式为
f(x)=a0+a1x+a2x2+…+a5x5,
令x=1,a0+a1+a2+a3+a4+a5=25+33,
令x=-1,a0-a1+a2-a3+a4-a5=-1,
两式相减得2(a1+a3+a5)=60,
故展开式中x的奇次幂项的系数之和为30.
11.已知(4 +)n展开式中的倒数第三项的二项式系数为45.
(1)求含有x3的项;
(2)求二项式系数最大的项.
解:(1)由已知得Cnn-2=45,即Cn2=45,
∴n2-n-90=0,解得n=-9(舍)或n=10,
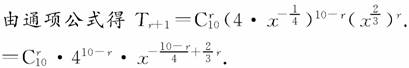
令-+r=3,得r=6,
∴含有x3的项是T7=C106·44·x3=53760x3.
(2)∵此展开式共有11项,
∴二项式系数最大项是第6项,
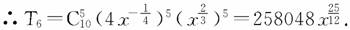
10.已知(a2+1)n展开式中各项系数之和等于(x2+)5的展开式的常数项,而(a2+1)n的展开式的二项式系数最大的项的系数等于54,求a的值.
解:由(x2+)5得,
Tr+1=C5r(x2)5-r()r=()5-r·C5r·x.
令Tr+1为常数项,则20-5r=0,
∴r=4,∴常数项T5=C54×=16.
又(a2+1)n展开式的各项系数之和等于2n.
由题意得2n=16,∴n=4.
由二项式系数的性质知,(a2+1)n展开式中二项式系数最大的项是中间项T3,∴C42a4=54,∴a=±.
9.若C233n+1=C23n+6(n∈N*)且(3-x)n=a0+a1x+a2x2+…+anxn,则a0-a1+a2-…+(-1)nan=________.
解析:3n+1=n+6或3n+1+n+6=23得n=4或n=(舍去).令x=-1,有44=a0-a1+a2-a3+a4=256.
答案:256
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com