
题目列表(包括答案和解析)
146.
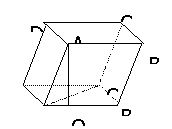
如图,在梯形ABCD中,AD//BC, ABC=900,AB=a,AD=3a,sin
ABC=900,AB=a,AD=3a,sin ADC=
ADC= ,又PA⊥平面ABCD,PA=a,求二面角P-CD-A的大小。(答案:arctg
,又PA⊥平面ABCD,PA=a,求二面角P-CD-A的大小。(答案:arctg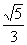 )
)
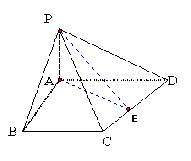

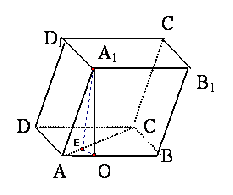
145. 如图,平行六面体ABCD-A1B1C1D1的底面为正方形,点A1在底面的射影O在AB上,已知侧棱A1A与底面ABCD成450角,A1A=a。求二面角A1-AC-B的平面角的正切值。(答案:
如图,平行六面体ABCD-A1B1C1D1的底面为正方形,点A1在底面的射影O在AB上,已知侧棱A1A与底面ABCD成450角,A1A=a。求二面角A1-AC-B的平面角的正切值。(答案: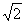 )
)
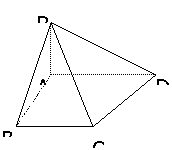
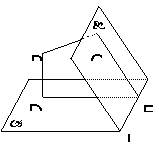
144. 如图,梯形ABCD中,BA⊥AD,CD⊥AD,AB=2,CD=4,P为平面ABCD外一点,平面PAD⊥平面ABCD,△PBC是边长为10的正三角形,求平面PAD与面PBC所成的角.
解法一:如图,延长DA、CB交于E, =
=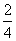 =
=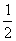 ,∴AB是△ECD的中位线,CB=BE=10.又△PCB为正△,易证△PCE为直角三角形,PE⊥PC.又平面PDA⊥平面ABCD,且CD⊥交线DA,∴CD⊥平面PDE.PE是PC在平面PDE内的射影,∴PE⊥PD(三垂线定理的逆定理).故∠CPD是D-PE-C的平面角.在Rt△CDP中,sin∠DPC=
,∴AB是△ECD的中位线,CB=BE=10.又△PCB为正△,易证△PCE为直角三角形,PE⊥PC.又平面PDA⊥平面ABCD,且CD⊥交线DA,∴CD⊥平面PDE.PE是PC在平面PDE内的射影,∴PE⊥PD(三垂线定理的逆定理).故∠CPD是D-PE-C的平面角.在Rt△CDP中,sin∠DPC=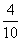 =
=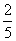 ,故二面角大小为arcsin
,故二面角大小为arcsin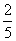 .
.

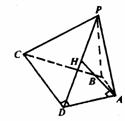 解法二:利用Scosθ=S′.如右图,
解法二:利用Scosθ=S′.如右图,
平面PAD⊥平面ABCD

 CD⊥AD,BA⊥AD
CD⊥AD,BA⊥AD
BA⊥平面PAD

CD⊥平面PAD
△PAD是△PBC在平面PDA内的射影.设面PDA与面PCB所成的二面角为θ,则S△PDA=S△PCB·cosθ.Rt△PAB中,PA=4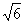 =AD;Rt△PDC中,PD=2
=AD;Rt△PDC中,PD=2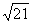 .
.
∴△PAD为等腰三角形且S△PAD=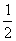 PD·AH=15
PD·AH=15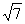 .
.
cosθ=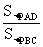 =
=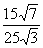 =
= ,
,
 θ=arccos=
θ=arccos= .
.
143.  如图,在平面角为600的二面角
如图,在平面角为600的二面角 -l-
-l-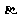 内有一点P,P到
内有一点P,P到 、
、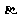 分别为PC=2cm,PD=3cm,则垂足的连线CD等于多少?(2)P到棱l的距离为多少?
分别为PC=2cm,PD=3cm,则垂足的连线CD等于多少?(2)P到棱l的距离为多少?
解析:对于本题若这么做:过C在平面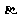 内作棱l的垂线,垂足为E,连DE,则
内作棱l的垂线,垂足为E,连DE,则 CED即为二面角的平面角。这么作辅助线看似简单,实际上在证明
CED即为二面角的平面角。这么作辅助线看似简单,实际上在证明 CED为二面角的平面角时会有一个很麻烦的问题,需要证明P、D、E、C四点共面。这儿,可以通过作垂面的方法来作二面角的平面角。
CED为二面角的平面角时会有一个很麻烦的问题,需要证明P、D、E、C四点共面。这儿,可以通过作垂面的方法来作二面角的平面角。
解:∵PC、PD是两条相交直线,
∴PC、PD确定一个平面 ,设
,设 交棱l于E,连CE、DE。
交棱l于E,连CE、DE。
∵PC⊥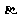 , ∴PC⊥l,
, ∴PC⊥l,
又∵PD⊥ ,∴PD⊥l。
,∴PD⊥l。
∴l⊥平面 ,则l⊥CE、DE,故
,则l⊥CE、DE,故 CED即为二面角的平面角,即
CED即为二面角的平面角,即 CED=600。
CED=600。
∴ CPD=1200,△PCD中,PD=3,PC=2,由余弦定理得CD=
CPD=1200,△PCD中,PD=3,PC=2,由余弦定理得CD=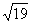 cm。由PD⊥DE,PC⊥CE可得P、D、E、C四点共圆,且PE为直径,由正弦定理得PE=2R=
cm。由PD⊥DE,PC⊥CE可得P、D、E、C四点共圆,且PE为直径,由正弦定理得PE=2R=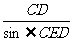 =
=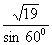 =
=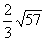 cm。
cm。
说明:三垂线定理及其逆定理是作二面角的平面角的最主要的方法,要引起重视。
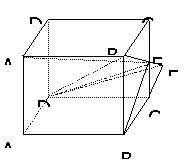
142. 如图,ABCD-A1B1C1D1是正方体,E是CC1的中点,求二面角B-B1E-D的余弦值。
解析:图中二面角的二个半平面分别为△DEB1所在的半平面和△BEB1所在的半平面,即正方体的右侧面,它们的交线即二面角的棱B1E。不难找到DC即为从其中的一个半平面出发,并且垂直于另一个半平面的直线。
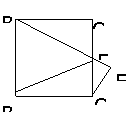 解: 由题意可得直线DC
解: 由题意可得直线DC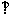 平面BEB1,且垂足为C,过C作CF
平面BEB1,且垂足为C,过C作CF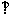 B1E于F(如图,F在B1E的延长线上),连DF,则由三垂线定理可得
B1E于F(如图,F在B1E的延长线上),连DF,则由三垂线定理可得 DFC即二面角的平面角。
DFC即二面角的平面角。
△B1C1E~△CFE,∴CF=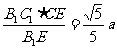 ;DF=
;DF=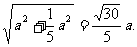
 ∴cos
∴cos DFC=
DFC= 。
。
即二面角的平面角的余弦值为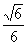 。
。
141.
已知菱形ABCD边长为a,且其一条对角线BD=a,沿对角线BD将 折起
折起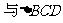 所在平面成直二面角,点E、F分别是BC、CD的中点。
所在平面成直二面角,点E、F分别是BC、CD的中点。
(1)求AC与平面AEF所成的角的余弦值
(2)求二面角A-EF-B的正切值。
(1) 解析::菱形ABCD的对角线 ,
,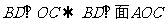
,中位线EF//BD,可知 面AOC,
面AOC, ,故面
,故面 ,这样AC在面AEF内的射影就是AG,
,这样AC在面AEF内的射影就是AG,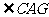 就是AC与平面AEF的成角,解三角形AOC可得
就是AC与平面AEF的成角,解三角形AOC可得 。
。
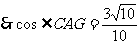
(2)分析:由前一小问的分析可知 ,
,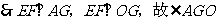
就是二面角A-EF-B的平面角,在 中,
中,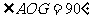 ,
,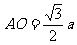 ,
,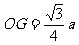 。
。
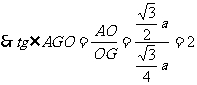

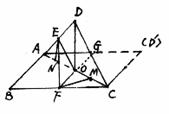
160. 把正方形ABCD沿对角线AC折成直二面角B-AC-D,E、F分别为AD、BC的中点,O为正方形的中心,求折起后∠EOF的大小
证明:过F作FM⊥AC于M,过E作EN⊥AC于N,则M,N分别为OC、AO的中点
解析:

158. 设△ABC内接于⊙O,其中AB为⊙O的直径,PA⊥平面ABC。
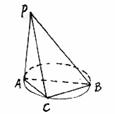 如图
如图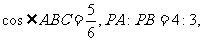 求直线PB和平面PAC所成角的大小
求直线PB和平面PAC所成角的大小

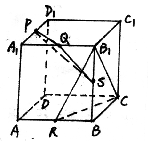 159.
如图,在正方体ABCD-A1B1C1D1中,已知P,Q,R,S分别为棱A1D1,A1B1,AB,BB1的中点,求证:平面PQS⊥平面B1RC.(12分)
159.
如图,在正方体ABCD-A1B1C1D1中,已知P,Q,R,S分别为棱A1D1,A1B1,AB,BB1的中点,求证:平面PQS⊥平面B1RC.(12分)
证明:连结BC1交B1C于O,则O为BC1的中点
连结RO,AC1,∵R是AB的中点 ∴RO∥AC1
∵P,Q分别为A1D1,A1B1的中点,易知A1C1⊥PQ
∴AC1⊥PQ(三垂线定理)

157.已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且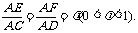
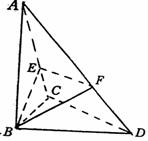 (Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
证明:(Ⅰ)∵AB⊥平面BCD, ∴AB⊥CD,
∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC.………………………………3分
又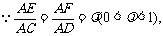
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC
(Ⅱ)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC.………………8分
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴
 由AB2=AE·AC 得
由AB2=AE·AC 得
故当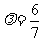 时,平面BEF⊥平面ACD.………………………………………………12分
时,平面BEF⊥平面ACD.………………………………………………12分
156. 有一矩形纸片ABCD,AB=5,BC=2,E,F分别是AB,CD上的点,且BE=CF=1,把纸片沿EF折成直二面角.
(1)求BD的距离;
(2)求证AC,BD交于一点且被这点平分.
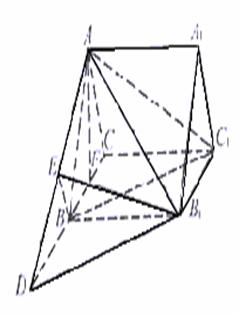
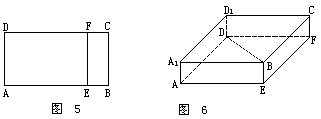
解析:将平面BF折起后所补形成长方体AEFD-A1BCD1,则BD恰好是长方体的一条对角线.
(1)解:因为AE,EF,EB两两垂直,
所以BD恰好是以AE,EF,EB为长、宽、高的长方体的对角线,
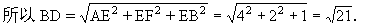 ................6分
................6分
(2)证明:因为AD 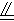 EF,EF
EF,EF 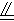 BC,所以AD
BC,所以AD 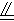 BC.
BC.
所以ACBD在同一平面内,
且四边形ABCD为平行四边形.
所以AC、BD交于一点且被这点平分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com