
题目列表(包括答案和解析)
7.设a、b是两条不同的直线,α、β是两个不同的平面,则下列四个命题 ( )
①若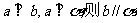 ②若
②若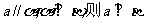
③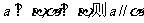 ④
④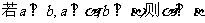
其中正确的命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
B 解析:注意①中b可能在α上;③中a可能在α上;④中b//α,或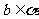 均有
均有 ,
,
故只有一个正确命题
6. 设A,B,C,D是空间不共面的四点,且满足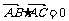 ,
,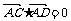 ,
,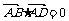 ,则△BCD是
,则△BCD是
(A)钝角三角形 (B)直角三角形 (C)锐角三角形 (D)不确定
C
解析:假设AB为a,AD为b,AC为c,且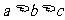 则,BD=
则,BD=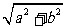 ,CD=
,CD=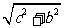 ,BC=
,BC=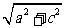 如图
如图 则BD为最长边,根据余弦定理
则BD为最长边,根据余弦定理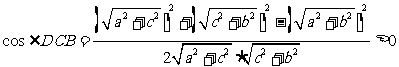
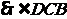 最大角为锐角。所以△BCD是锐角三角形。
最大角为锐角。所以△BCD是锐角三角形。
5. 在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是
(A)4条 (B)6条 (C)8条 (D)10条
C
解析:如图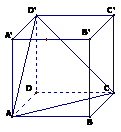 这样的直线有4条,另外,这样的
这样的直线有4条,另外,这样的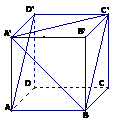 直线也有4条,共8条。
直线也有4条,共8条。
4. 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线AB与直线B1C1的距离相等,则动点P所在曲线的形状为
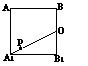



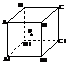
C
解析: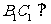 平面AB1
平面AB1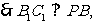 ,如图:
,如图: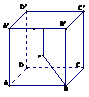 P点到定点B的距离与到定直线AB的距离相等,建立坐标系画图时可以以点B1B的中点为原点建立坐标系。
P点到定点B的距离与到定直线AB的距离相等,建立坐标系画图时可以以点B1B的中点为原点建立坐标系。
3. 有三个平面 ,β,γ,下列命题中正确的是
,β,γ,下列命题中正确的是
(A)若 ,β,γ两两相交,则有三条交线 (B)若
,β,γ两两相交,则有三条交线 (B)若 ⊥β,
⊥β,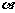 ⊥γ,则β∥γ
⊥γ,则β∥γ
(C)若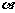 ⊥γ,β∩
⊥γ,β∩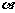 =a,β∩γ=b,则a⊥b (D)若
=a,β∩γ=b,则a⊥b (D)若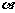 ∥β,β∩γ=
∥β,β∩γ= ,则
,则 ∩γ=
∩γ=
D
解析:A项:如正方体的一个角,三个平面相交,只有一条交线。
B项:如正方体的一个角,三个平面互相垂直,却两两相交。
C项:如图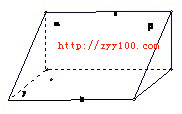
2. 下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是
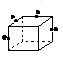
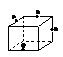
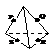
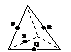
(A) (B) (C) (D)
D
解析: A项: 底面对应的中线,中线平行QS,PQRS是个梯形
底面对应的中线,中线平行QS,PQRS是个梯形
B项: 如图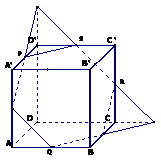
C项:是个平行四边形
D项:是异面直线。
1、二面角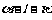 是直二面角,
是直二面角,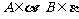 ,设直线
,设直线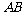 与
与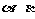 所成的角分别为∠1和∠2,则
所成的角分别为∠1和∠2,则
(A)∠1+∠2=900 (B)∠1+∠2≥900 (C)∠1+∠2≤900 (D)∠1+∠2<900
解析:C
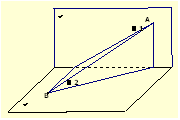 如图所示作辅助线,分别作两条与二面角的交线垂直的线,则∠1和∠2分别为直线AB与平面
如图所示作辅助线,分别作两条与二面角的交线垂直的线,则∠1和∠2分别为直线AB与平面 所成的角。根据最小角定理:斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
所成的角。根据最小角定理:斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
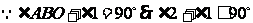
150. 在矩形ABCD中,AB=a,AD=2b,a<b,E、F分别是
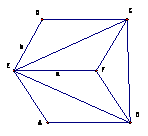 AD、BC的中点,以EF为折痕把四边形EFCD折起,
AD、BC的中点,以EF为折痕把四边形EFCD折起,
当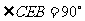 时,二面角C-EF-B的平面角的余
时,二面角C-EF-B的平面角的余
弦值等于 ( )
A.0 B. C.
C.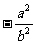 D.
D.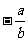
解析:由图可知 CE=BE=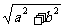 当
当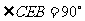 时,CB=
时,CB=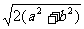 。
。 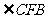 为所求平面角,由余弦定理得cos
为所求平面角,由余弦定理得cos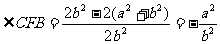 。 选(C)。
。 选(C)。
148.
矩形ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,
使点A在平面BCD上的射影A′落在BC上,求二面角A-BC--C的大小。
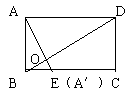
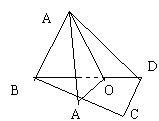 这是一道由平面图形折叠成立体图形的问题,解决问题的关键在
于搞清折叠前后“变”与“不变”。结果在平面图形中过A作AE⊥BD交BD于O、交BC于E,则折叠后OA、OE与BD的垂直关系不变。但OA与OE此时变成相交两线段并确定一平面,此平面必与棱垂直。由特征Ⅱ可知,面AOE与面ABD、面CBD的交线OA与OE所成的角,即为所求二面角的平面角。另外,A在面BCD上的射影必在OE所在的直线上,又题设射影落在BC上,所以E点就是A′,这样的定位给下面的定量提供了优质服务。事实上,AO=AB·AD/BD=3*4/5=12/5,OA′=OE=BO·tgc∠CBD,而BO=AB2/BD=9/5, tg∠CBD,故OA′=27/20。在Rt△AA′O中,∠AA′O=90°所以cos∠AOA′=A′O/AO=9/16,ty∠AOA′=arccos9/16即所求的二面arccos9/16。
149. 将边长为
这是一道由平面图形折叠成立体图形的问题,解决问题的关键在
于搞清折叠前后“变”与“不变”。结果在平面图形中过A作AE⊥BD交BD于O、交BC于E,则折叠后OA、OE与BD的垂直关系不变。但OA与OE此时变成相交两线段并确定一平面,此平面必与棱垂直。由特征Ⅱ可知,面AOE与面ABD、面CBD的交线OA与OE所成的角,即为所求二面角的平面角。另外,A在面BCD上的射影必在OE所在的直线上,又题设射影落在BC上,所以E点就是A′,这样的定位给下面的定量提供了优质服务。事实上,AO=AB·AD/BD=3*4/5=12/5,OA′=OE=BO·tgc∠CBD,而BO=AB2/BD=9/5, tg∠CBD,故OA′=27/20。在Rt△AA′O中,∠AA′O=90°所以cos∠AOA′=A′O/AO=9/16,ty∠AOA′=arccos9/16即所求的二面arccos9/16。
149. 将边长为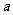 的正方形
的正方形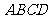 沿对角线
沿对角线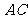 折起,使得
折起,使得 ,则三棱锥
,则三棱锥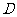 -
-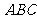 的体积为 ( )
的体积为 ( )
A. 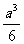 B.
B.
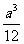 C.
C.
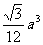 D.
D. 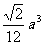
D
解析:取BD的中点为O,BD⊥平面OAC,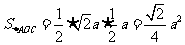 ,则
,则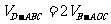 =
=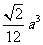 。选D
。选D
147.
已知Rt△ABC的两直角边AC=2,BC=3,P为斜边上一
点,沿CP将此直角三角形折成直二面角A-CP-B,当AB=71/2时,求二面角P-AC-B的大小。
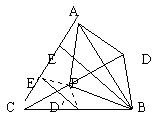
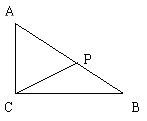 作法一:∵A-CP-B为直角二面角,
∴过B作BD⊥CP交CP的延长线于D,则BD⊥DM APC。
∴过D作DE ⊥AC,垂足为E,连BE。
∴∠DEB为二面角A-CP-B的平面角。
作法二:过P点作PD′⊥PC交BC于D′,则PD′⊥面APC。
∴过D′作D′E′⊥AC,垂足为E′,边PE′,
∴∠D′E′P为二面角P-AC-B的平面角。
作法一:∵A-CP-B为直角二面角,
∴过B作BD⊥CP交CP的延长线于D,则BD⊥DM APC。
∴过D作DE ⊥AC,垂足为E,连BE。
∴∠DEB为二面角A-CP-B的平面角。
作法二:过P点作PD′⊥PC交BC于D′,则PD′⊥面APC。
∴过D′作D′E′⊥AC,垂足为E′,边PE′,
∴∠D′E′P为二面角P-AC-B的平面角。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com