
题目列表(包括答案和解析)
19.线段OA,OB,OC不共面, AOB=
AOB= BOC=
BOC= COA=60
COA=60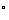 ,OA=1,OB=2,OC=3,则△ABC是
,OA=1,OB=2,OC=3,则△ABC是
( )
A.等边三角形 B非等边的等腰三角形
C.锐角三角形 D.钝角三角形
解析:B. 设 AC=x,AB=y,BC=z,由余弦定理知:x2=12+32-3=7,y2=12+22-2=3,z2=22+32-6=7。
∴ △ABC是不等边的等腰三角形,选(B).
17.如图,点P、Q、R、S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的一个图是( )
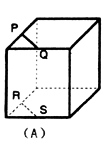
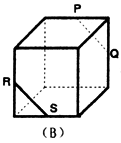
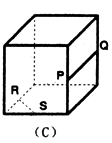
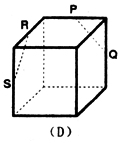
解析:C A,B选项中的图形是平行四边形,而D选项中可见图: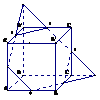
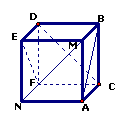
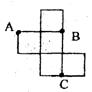 18.如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC等于 ( )
18.如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC等于 ( )
A.45° B.60°
C.90° D.120°
解析:B 如图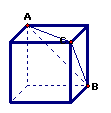
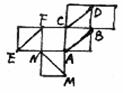
★右图是一个正方体的展开图,在原正方体中,有下列命题:
①AB与CD所在直线垂直; ②CD与EF所在直线平行
③AB与MN所在直线成60°角; ④MN与EF所在直线异面
其中正确命题的序号是 ( )
A.①③ B.①④ C.②③ D.③④
解析:D
15.若 为异面直线,直线c∥a,则c与b的位置关系是 ( )
为异面直线,直线c∥a,则c与b的位置关系是 ( )
A.相交 B.异面 C.平行 D. 异面或相交
解析:D 如正方体的棱长。
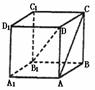 16.在正方体A1B1C1D1-ABCD中,AC与B1D所成的角的大小为 ( )
16.在正方体A1B1C1D1-ABCD中,AC与B1D所成的角的大小为 ( )
A.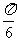 B.
B.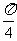
C.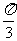 D.
D.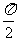
解析:D B1D在平面AC上的射影BD与AC垂直,根据三垂线定理可得。
B1D在平面AC上的射影BD与AC垂直,根据三垂线定理可得。
14.空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为( )
A.3 B.1或2 C.1或3 D.2或3
解析:C 如三棱柱的三个侧面。
13. 已知直线m、n及平面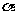 ,其中m∥n,那么在平面
,其中m∥n,那么在平面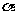 内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.其中正确的是
内到两条直线m、n距离相等的点的集合可能是:(1)一条直线;(2)一个平面;(3)一个点;(4)空集.其中正确的是
.
解析:(1)成立,如m、n都在平面内,则其对称轴符合条件;(2)成立,m、n在平面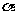 的同一侧,且它们到
的同一侧,且它们到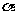 的距离相等,则平面
的距离相等,则平面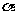 为所求,(4)成立,当m、n所在的平面与平面
为所求,(4)成立,当m、n所在的平面与平面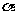 垂直时,平面
垂直时,平面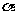 内不存在到m、n距离相等的点
内不存在到m、n距离相等的点
12. 设有如下三个命题:甲:相交直线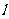 、m都在平面α内,并且都不在平面β内;乙:直线
、m都在平面α内,并且都不在平面β内;乙:直线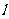 、m中至少有一条与平面β相交;丙:平面α与平面β相交.
、m中至少有一条与平面β相交;丙:平面α与平面β相交.
当甲成立时,
A.乙是丙的充分而不必要条件 B.乙是丙的必要而不充分条件
C.乙是丙的充分且必要条件 D.乙既不是丙的充分条件又不是丙的必要条件
解析:当甲成立,即“相交直线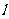 、m都在平面α内,并且都不在平面β内”时,若“
、m都在平面α内,并且都不在平面β内”时,若“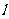 、m中至少有一条与平面β相交”,则“平面α与平面β相交.”成立;若“平面α与平面β相交”,则“
、m中至少有一条与平面β相交”,则“平面α与平面β相交.”成立;若“平面α与平面β相交”,则“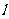 、m中至少有一条与平面β相交”也成立.选(C).
、m中至少有一条与平面β相交”也成立.选(C).
11. 正四面体棱长为1,其外接球的表面积为
A.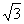 π B.
π B.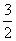 π
C.
π
C.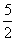 π D.3π
π D.3π
解析:正四面体的中心到底面的距离为高的1/4。(可连成四个小棱锥得证
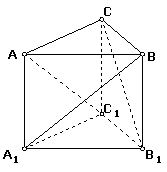
10. 已知正三棱柱ABC-A1B1C1中,A1B⊥CB1,则A1B与AC1
所成的角为
(A)450 (B)600
(C)900 (D)1200
C解析:作CD⊥AB于D,作C1D1⊥A1B1于D1,连B1D、AD1,易知ADB1D1是平行四边形,由三垂线定理得A1B⊥AC1,选C。
9. 对于平面M与平面N, 有下列条件: ①M、N都垂直于平面Q; ②M、N都平行于平面Q; ③ M内不共线的三点到N的距离相等; ④ l, M内的两条直线, 且l // M, m // N; ⑤ l, m是异面直线,且l // M, m // M; l // N, m // N, 则可判定平面M与平面N平行的条件的个数是 ( )
 A.1 B.2 C.3 D.4
A.1 B.2 C.3 D.4
只有②、⑤能判定M//N,选B
8.如图所示,已知正四棱锥S-ABCD侧棱长为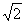 ,底
,底
 面边长为
面边长为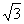 ,E是SA的中点,则异面直线BE与SC
,E是SA的中点,则异面直线BE与SC
所成角的大小为 ( )
A.90° B.60°
C.45° D.30°
B 解析:平移SC到 ,运用余弦定理可算得
,运用余弦定理可算得
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com