9．已知定义在区间[0,3]上的函数f(x)＝kx²－2kx的最大值为3，那么实数k的取值范围为________．

解析：∵f(x)＝k(x－1)²－k，

(1)当k>0时，二次函数图象开口向上，当x＝3时，f(x)有最大值，f(3)＝k·3²－2k×3＝3k＝3⇒k＝1；

(2)当k<0时，二次函数图象开口向下，当x＝1时，f(x)有最大值，f(1)＝k－2k＝－k＝3⇒k＝－3.

(3)当k＝0时，显然不成立．

故k的取值集合为{1，－3}．

答案：{1，－3}

8．方程x²－mx+1＝0的两根为α、β，且α＞0,1＜β＜2，则实数m的取值范围是________．

解析：∵∴m＝β+，∵β∈(1,2)且函数m＝β+在(1,2)上是增函数，∴1+1＜m＜2+，即m∈(2，)．

答案：(2，)

7．已知函数f(x)＝x²－2x+2的定义域和值域均为[1，b]，则b＝________.

解析：∵f(x)＝(x－1)²+1，∴f(x)在[1，b]上是增函数，

f(x)_max＝f(b)，∴f(b)＝b，∴b²－2b+2＝b，

∴b²－3b+2＝0，∴b＝2或1(舍)．

答案：2

6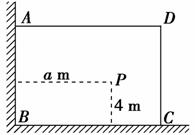．如图，有一直角墙角，两边的长度足够长，在P处有一棵树与两墙的距离分别为a m(0＜a＜12)、4 m，不考虑树的粗细．现在想用16 m长的篱笆，借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的面积为S m²，S的最大值为f(a)，若将这颗树围在花圃内，则函数u＝f(a)的图象大致是(　)

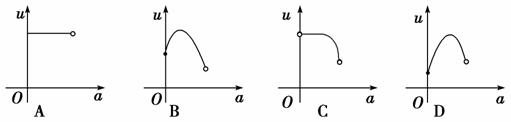
解析：选C.据题意设BC＝x，则DC＝16－x，要使树围在花圃内，需⇒a≤x≤12，此时花圃的面积f(x)＝x(16－x)＝－(x－8)²+64(a≤x≤12)，当8＜a<12时，有f(a)＝－a²+16a，当0＜a≤8时有f(a)＝f(8)＝64，综上所述可得：f(a)＝，作出图形易知C选项正确．

5．已知函数f(x)＝x²+ax+b，且f(x+2)是偶函数，则f(1)，f()，f()的大小关系是(　)

A．f()＜f(1)＜f()　　　　　 B．f(1)＜f()＜f()

C．f()＜f(1)＜f()　　　　 　D．f()＜f()＜f(1)

解析：选A.由f(x+2)是偶函数可知函数f(x)＝x²+ax+b关于直线x＝2对称，所以f(1)＝f(3)，又该函数图象开口向上，当x＞2时单调递增，故f()＜f(3)＝f(1)＜f()，故答案为A.

4．已知函数y＝ax²+bx+c，如果a＞b＞c，且a+b+c＝0，则它的图象是(　)

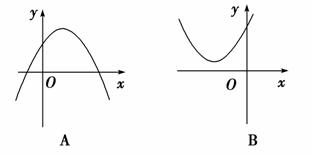
解析：选D.∵a＞b＞c，且a+b+c＝0，得a＞0，c＜0(用反证法可得)，∴f(0)＝c＜0，∴只能是D.

3．若f(x)＝x²－x+a，f(－m)＜0，则f(m+1)的值为(　)

A．正数　 　　　　　　　　　B．负数

C．非负数　 　　　　　　　　D．与m有关

解析：选B.法一：∵f(x)＝x²－x+a的对称轴为x＝，

而－m，m+1关于对称，

∴f(m+1)＝f(－m)＜0，故选B.

法二：∵f(－m)＜0，∴m²+m+a＜0，

∴f(m+1)＝(m+1)²－(m+1)+a＝m²+m+a＜0.故选B.

2．若f(x)＝x²－ax+1有负值，则实数a的取值范围是(　)

A．a>2或a<－2　 　　　　　B．－2<a<2

C．a≠±2　 　　　　　　　　D．1<a<3

解析：选A.f(x)有负值，则必须满足f(x)的图象与x轴有两个不同的交点，其充要条件是：Δ＝(－a)²－4>0，a²>4即a>2或a<－2.

1．(2008年高考辽宁卷)若函数y＝(x+1)(x－a)为偶函数，则a等于(　)

A．－2　 　　　　　　　　　　B．－1

C．1　 　　　　　　　　　　　D．2

解析：选C.∵y＝(x+1)(x－a)＝x²+(1－a)x－a是偶函数

∴1－a＝0，∴a＝1，故选C.

20．若a，b，l是两两异面的直线，a与b所成的角是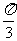，l与a、l与b所成的角都是，

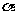则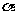的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

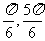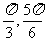　　 A．[]　　　 B．[]　　　　 C．[]　　　 D．[]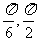

解析：D

解 当l与异面直线a，b所成角的平分线平行或重合时，a取得最小值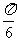，当l与a、b的公垂线平行时，a取得最大值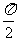，故选(D)．