4．(2008年高考海南、宁夏卷)由直线x＝，x＝2，曲线y＝及x轴所围成图形的面积为(　)

A.　 　　　　　　　　B.

C.ln2　 　　　　　　　D．2ln2

3．一物体的下落速度为v(t)＝9.8t+6.5(单位：米/秒)，则下落后第二个4秒内经过的路程是(　)

A．249米　 　　　　　　B．261.2米

C．310.3米　 　　　　　D．450米

解析：选B.所求路程为(9.8t+6.5)dt

＝(4.9t²+6.5t)|

＝4.9×64+6.5×8－4.9×16－6.5×4

＝313.6+52－78.4－26

＝261.2(米)．

2．函数y＝(cost+t²+2)dt(x>0)(　)

A．是奇函数　 　　　　　B．是偶函数

C．非奇非偶函数　 　　　D．以上都不正确

解析：选A.y＝|＝2sinx++4x，为奇函数．

1．已知f(x)为偶函数且 f(x)dx＝8，则f(x)dx等于(　)

A．0　 　　　　　　　　　B．4

C．8 　　　　　　　　　D．16

解析：选D.原式＝f(x)dx+f(x)dx，

∵原函数为偶函数，

∴在y轴两侧的图象对称．

∴对应的面积相等．故选D.

6．设y＝f(x)是二次函数，方程f(x)＝0有两个相等的实根，且f′(x)＝2x－2.

(1)求y＝f(x)的表达式；

(2)求y＝f(x)的图象与两坐标轴所围成图形的面积．

解：(1)设f(x)＝ax²+bx+c(a≠0)，

则f′(x)＝2ax+b.又f′(x)＝2x－2，

所以a＝1，b＝－2，即f(x)＝x²－2x+c.

又方程f(x)＝0有两个相等实根，

所以Δ＝4－4c＝0，即c＝1.

故f(x)＝x²－2x+1.

(2)依题意，所求面积为

S＝(x²－2x+1)dx＝(x³－x²+x)|＝.

练习

5.已知函数f(x)＝3x²+2x+1，若f(x)dx＝2f(a)成立，则a＝________.

解析： (3x²+2x+1)dx＝(x³+x²+x)| ＝4，

所以2(3a²+2a+1)＝4，即3a²+2a－1＝0，

解得a＝－1或a＝.

答案：－1或

4．若等比数列{a_n}的首项为，且a₄＝ (1+2x)dx，则公比等于________．

解析：本题考查定积分运算及等比数列基本量的求解．由已知得a₄＝(x+x²)|＝18，故q³＝＝27⇒q＝3.

答案：3

3．设函数f(x)＝x^m+ax的导函数f′(x)＝2x+1，则

f(－x)dx的值等于(　)

A.　　　　　　　　　　　 　B.

C.　 　　　　　　　　　　　　D.

解析：选A.由于f(x)＝x^m+ax的导函数为f′(x)＝2x+1，所以f(x)＝x²+x，于是f(－x)dx＝ (x²－x)dx＝＝.

2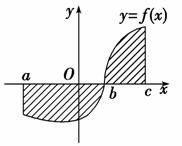．(原创题)用S表示图中阴影部分的面积，则S的值是(　)

A．f(x)dx

B．|f(x)dx|

C．f(x)dx+f(x)dx

D．f(x)dx－f(x)dx

解析：选D.由定积分的几何意义知选项D正确．

12．若f(x)＝x²－x+b，且f(log₂a)＝b，log₂[f(a)]＝2(a≠1)．

(1)求f(log₂x)的最小值及对应的x值；

(2)x取何值时，f(log₂x)>f(1)且log₂[f(x)]<f(1)．

解：(1)∵f(x)＝x²－x+b，

∴f(log₂a)＝(log₂a)²－log₂a+b.由已知(log₂a)²－log₂a+b＝b，

∴log₂a(log₂a－1)＝0.

∵a≠1，∴log₂a＝1，∴a＝2.

又log₂[f(a)]＝2，∴f(a)＝4.

∴a²－a+b＝4，∴b＝4－a²+a＝2.

故f(x)＝x²－x+2.

从而f(log₂x)＝(log₂x)²－log₂x+2＝(log₂x－)²+.

∴当log₂x＝，即x＝时，f(log₂x)有最小值.

(2)由题意⇒

⇒0<x<1.