1．(2008年高考广东卷)记等差数列{a_n}的前n项和为S_n.若S₂＝4，S₄＝20，则该数列的公差d＝(　)

A．7　 　　　　　　　　B．6

C．3　 　　　　　　　　D．2

解析：选C.S₂＝4，S₄＝20⇒a₃+a₄＝16，又a₁+a₂＝4，a₃+a₄－a₁－a₂＝12,4d＝12，d＝3.故选C.

\x(　康托尔与集合论(四2.设数列{a_n}的前n项和为S_n，且a_n＝－2n+1，则数列{}的前11项和为(　)

A．－45　 　　　　　　　B．－50

C．－55　 　　　　　　　D．－66

解析：选D.S_n＝＝－n²，即＝－n，则数列{}的前11项和为－1－2－3－4－…－11＝－66.

6．(2009年高考全国卷Ⅱ)已知等差数列{a_n}中，a₃a₇＝－16，a₄+a₆＝0，求{a_n}的前n项和S_n.

解：设{a_n}的公差为d，则

即

解得或

因此S_n＝－8n+n(n－1)＝n(n－9)，

　 或S_n＝8n－n(n－1)＝－n(n－9)．

练习

5．已知S_n是等差数列{a_n}的前n项和，且S₁＝1，S₁₉＝95，则a₁₉＝________，S₁₀＝________.

解析：a₁＝S₁＝1，S₁₉＝×19＝95⇒＝5⇒a₁₉＝10－1＝9，S₁₀＝×10＝×10＝×10＝30.

答案：9　30

4．(2009年高考陕西卷)设等差数列{a_n}的前n项和为S_n，若a₆＝S₃＝12，则{a_n}的通项a_n＝________.

解析：设等差数列首项为a₁，公差为d，

则

即

∴

a_n＝a₁+(n－1)d＝2n.

答案：2n

3．(2009年高考安徽卷)已知{a_n}为等差数列，a₁+a₃+a₅＝105，a₂+a₄+a₆＝99，则a₂₀等于(　)

A．－1 　　　　　　　　　　B．1

C．3　 　　　　　　　　　　D．7

解析：选B.由已知得a₁+a₃+a₅＝3a₃＝105，

a₂+a₄+a₆＝3a₄＝99，

∴a₃＝35，a₄＝33，∴d＝－2.

∴a₂₀＝a₃+17d＝35+(－2)×17＝1.

2．(原创题)在等差数列{a_n}中，若a₁+a₅+a₉＝4π，则tan(a₂+a₈)的值是(　)

A．－ 　　　　　　　　　B．－1

C．－　 　　　　　　　　D.

解析：选A.根据等差数列等差中项的性质可得，a₁+a₅+a₉＝3a₅＝4π，所以a₅＝，

又a₂+a₈＝2a₅＝，

故tan(a₂+a₈)＝tan＝tan＝－，答案为A.

1．数列{a_n}中，a_n+1＝a_n+2(n∈N^*)，则点A₁(1，a₁)，A₂(2，a₂)，…，A_n(n，a_n)分布在(　)

A．直线上，且直线的斜率为－2

B．抛物线上，且抛物线的开口向下

C．直线上，且直线的斜率为2

D．抛物线上，且抛物线的开口向上

解析：选C.∵＝a_n－a_n－1＝2(n≥2)，

∴A₁，A₂，A₃，…，A_n在斜率为2的直线上．

7．已知a∈[0，]，则当ʃa0(cosx－sinx)dx取最大值时，a＝________.

解析：(cosx－sinx)dx＝(sinx+cosx)|＝sina+cosa－(sin0+cos0)＝sin(a+)－1，当a＝时，(cosx－sinx)dx取最大值－1.

6．函数f(x)＝的图象与x轴所围成的封闭图形的面积为(　)

A.　 　　　　　　　　　　　　B．1

C．2　 　　　　　　　　　　　D.

解析：选A.作出图象可知：S＝－1(x+1)dx+ cosxdx＝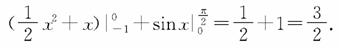　　

5．若a＝x²dx，b＝x³dx，c＝sinxdx，则a、b、c的大小关系是(　)

A．a<c<b　 　　　　　　　　B．a<b<c

C．c<b<a　 　　　　　　　　D．c<a<b

解析：选D.a＝x²dx＝x³|＝，

b＝x³dx＝x⁴|4，

c＝sinxdx＝－cosx|＝1－cos2，

因为1<1－cos2<2，所以c<a<b.