3．在正项数列{a_n}中，a₁＝2，点(，)(n≥2)在直线x－y＝0上，则数列{a_n}的前n项和S_n等于(　)

A．2ⁿ－1　 　　　　　　　B．2ⁿ⁺¹－2

C．2－　 　　　　　　D．2－

解析：选B.由点(，)(n≥2)在直线x－y＝0上得，－＝0，即a_n＝2a_n－1.又a₁＝2，所以当n≥2时，＝2，故数列{a_n}是以2为首项，以2为公比的等比数列．所以S_n＝＝2ⁿ⁺¹－2，故选B.

2．(2009年高考广东卷)已知等比数列{a_n}满足a_n>0，n＝1,2，…，且a₅·a_2n－5＝2²ⁿ(n≥3)，则当n≥1时，log₂a₁+log₂a₃+…+log₂a_2n－1＝(　)

A．n(2n－1)　 　　　　　　B．(n+1)²

C．n² 　　　　　　　　　D．(n－1)²

解析：选C.由题知a_n＝2ⁿ，log₂a_2n－1＝2n－1，

log₂a₁+log₂a₃+…+log₂a_2n－1＝1+3+…+(2n－1)＝n².

1．(2008年高考全国卷Ⅰ)已知等比数列{a_n}满足a₁+a₂＝3，a₂+a₃＝6，则a₇＝(　)

A．64　　　　　B．81

C．128　 　　　　　　　　　D．243

解析：选A.设首项为a₁，公比为q，

则⇒，

∴a₇＝a₁q⁶＝64.

9．设等差数列{a_n}、{b_n}的前n项和分别为S_n、T_n，若对任意自然数n都有＝，则+的值为________．

解析：∵{a_n}，{b_n}为等差数列，

∴+＝+＝＝.

∵＝＝＝＝，∴＝.

8．在等差数列{a_n}中，|a₃|＝|a₉|，公差d<0，则使前n项和S_n取得最大值的自然数n是________．

解析：∵d<0，|a₃|＝|a₉|，∴a₃＝－a₉，

∴a₁+2d＝－a₁－8d，

∴a₁+5d＝0，∴a₆＝0，

∴a_n>0(1≤n≤5)，

∴S_n取得最大值时的自然数n是5或6.

答案：5或6

7．设S_n为等差数列{a_n}的前n项和，S₄＝14，S₁₀－S₇＝30，则S₉＝______.

解析：设首项为a₁，公差为d，由S₄＝14得

4a₁+d＝14.①

由S₁₀－S₇＝30得3a₁+24d＝30，即a₁+8d＝10.②

联立①②得a₁＝2，d＝1.∴S₉＝54.

答案：54

6．设S_n是等差数列{a_n}的前n项和，若a₁>0，S₈＝S₁₃，S_k＝0，则k的值为(　)

A．18　 　　　　　　B．19

C．20　 　　　　　　D．21

解析：选D.∵S_n是等差数列{a_n}的前n项和，

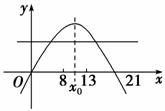
∴S_n＝An²+Bn，S_n的图象为开口向下的抛物线y＝Ax²+Bx上横坐标为正整数的点，抛物线的对称轴为x₀＝＝，点(0,0)与(21,0)关于直线x₀＝对称，∴S₂₁＝0，即k＝21.

5．已知数列{a_n}是正项等差数列，给出下列判断：

①a₂+a₈＝a₄+a₆；②a₄·a₆≥a₂·a₈；③a₅²≤a₄·a₆；④a₂+a₈≥2.其中有可能正确的是(　)

A．①④　 　　　　　　B．①②④

C．①③　 　　　　　　D．①②③

解析：选B.∵数列{a_n}是正项等差数列，

∴①a₂+a₈＝a₄+a₆正确；

又∵a₂+a₈＝a₄+a₆≥2，

∴④正确；

又∵a₄·a₆－a₂·a₈＝(a₁+3d)(a₁+5d)－(a₁+d)(a₁+7d)＝8d²≥0(其中d为公差)，

∴②正确；同理可判断出③不正确，故选B.

4．已知等差数列{a_n}中，a₁＝11，前7项的和S₇＝35，则前n项和S_n中(　)

A．前6项和最小　 　　　B．前7项和最小

C．前6项和最大　 　　　D．前7项和最大

解析：选C.由等差数列求和公式S₇＝7×11+d＝35可得d＝－2，则a_n＝11+(n－1)×(－2)＝13－2n，要使前n项和最大，只需a_n≥0即可，故13－2n≥0，解之得n≤6.5，故前6项的和最大．

3．设S_n是等差数列{a_n}的前n项和，若＝，则等于(　)

A．1　 　　　　　　　　B．－1

C．2　 　　　　　　　　D.

解析：选A.由已知得：＝＝＝×＝1.