1.

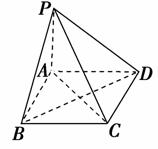
PA垂直于正方形ABCD所在平面，连结PB，PC，PD，AC，BD，则下列垂直关系正确的是(　)

①面PAB⊥面PBC　②面PAB⊥面PAD

③面PAB⊥面PCD　④面PAB⊥面PAC

A．①②　 　　　　　　　　B．①③

C．②③ 　　　　　　　　　D．②④

解析：选A.易证BC⊥平面PAB，

则平面PAB⊥平面PBC；

又AD∥BC，

故AD⊥平面PAB，

则平面PAD⊥平面PAB，

因此选A.

5．(原创题)棱长为2的正方体ABCD－A₁B₁C₁D₁中，M是棱AA₁的中点，过C、M、D₁作正方体的截面，则截面的面积是__________．

解析：由面面平行的性质知截面与面AB₁的交线MN是△AA₁B的中位线，所以截面是梯形CD₁MN，易求其面积为.

4.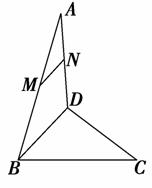 如图，在空间四边形ABCD中，M∈AB，N∈AD，若＝，则直线MN与平面BDC的位置关系是__________．

解析：在平面ABD中，＝，

∴MN∥BD.

又MN⊄平面BCD，BD⊂平面BCD，

∴MN∥平面BCD.

答案：平行

3．(2010年启东中学质检)已知m、n是不重合的直线，α、β是不重合的平面，有下列命题：

①若m⊂α，n∥α，则m∥n；

②若m∥α，m∥β，则α∥β；

③若α∩β＝n，m∥n，则m∥α且m∥β；

④若m⊥α，m⊥β，则α∥β.

其中真命题的个数是(　)

A．0　 　　　　　　　　　　　　B．1

C．2 　　　　　　　　　　　　D．3

答案：B

2．(2009年高考福建卷)设m，n是平面α内的两条不同直线；l₁，l₂是平面β内的两条相交直线．则α∥β的一个充分而不必要条件是(　)

A．m∥β且l₁∥α 　　　　　　　B．m∥l₁且n∥l₂

C．m∥β且n∥β 　　　　　　　D．m∥β且n∥l₂

解析：选B.∵m∥l₁，且n∥l₂，又l₁与l₂是平面β内的两条相交直线，∴α∥β，而当α∥β时不一定推出m∥l₁且n∥l₂，可能异面．故选B.

1．已知α∥β，a⊂α，B∈β，则在β内过点B的所有直线中(　)

A．不一定存在与a平行的直线

B．只有两条与a平行的直线

C．存在无数条与a平行的直线

D．存在唯一一条与a平行的直线

解析：选D.B点与a确定一平面γ与β相交，设交线为b，则a∥b.

5．两封信随机投入A、B、C三个空邮箱，则A邮箱的信件数ξ的数学期望Eξ＝________.

解析：当ξ＝1时，P(ξ＝1)＝＝，P(ξ＝2)＝＝，

∴Eξ＝1×+2×＝.

4．(原创题)若p为非负实数，随机变量ξ的概率分布列如下表，则Eξ的最大值为________，Dξ的最大值为________.

解析：Eξ＝p+1≤(0≤p≤)；Dξ＝－p²－p+1≤1.

答案：　1

3．若X-B(n，p)，且EX＝6，DX＝3，则P(X＝1)的值为(　)

A．3·2^－2 　　　　　　　　　　B．2^－4

C．3·2^－10　 　　　　　　　　　D．2^－8

解析：选C.EX＝np＝6，DX＝np(1－p)＝3，∴p＝，n＝12，

则P(X＝1)＝C₁₂¹··()¹¹＝3·2^－10.

2．(2008年高考湖南卷)设随机变量ξ服从正态分布N(2,9)，若P(ξ>c+1)＝P(ξ<c－1)，则c＝(　)

A．1 　　　　　　　　　　　B．2

C．3　 　　　　　　　　　　　D．4

解析：选B.∵μ＝2，由正态分布的定义知其函数图象关于x＝2对称，于是＝2，∴c＝2.故选B.