5．在二面角α－l－β的两个面α，β内，分别有直线a，b，它们与棱l都不垂直，则(　)

A．当该二面角是直二面角时，可能a∥b，也可能a⊥b

B．当该二面角是直二面角时，可能a∥b，但不可能a⊥b

C．当该二面角不是直二面角时，可能a∥b，但不可能a⊥b

D．当该二面角不是直二面角时，不可能a∥b，也不可能a⊥b

解析：选B.当该二面角为直二面角时(如图)，若a⊥b，∵b与l不垂直，在b上取点A，过A作AB⊥l，AB∩b＝A，

由⇒⇒a⊥β⇒a⊥l.

这和a与l不垂直相矛盾．

∴不可能a⊥b.故A错误，

∴B正确．

4.如图，已知△ABC为直角三角形，其中∠ACB=90°，M为AB中点，PM垂直于△ABC所在平面，那么(　)

A．PA＝PB>PC

B．PA＝PB<PC

C．PA＝PB＝PC

D．PA≠PB≠PC

解析：选C.∵M是Rt△ABC斜边AB的中点，

∴MA＝MB＝MC.

又∵PM⊥平面ABC，∴MA、MB、MC分别是PA、PB、PC在平面ABC上的射影．∴PA＝PB＝PC.应选C.

3.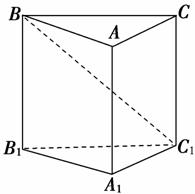如图，在斜三棱柱ABC-A₁B₁C₁中，∠BAC=90°，BC₁⊥AC，则C₁在底面ABC上的射影H必在(　)

A．直线AB上

B．直线BC上

C．直线AC上

D．△ABC内部

解析：选A.∵BA⊥AC，BC₁⊥AC，BA∩BC₁＝B，

∴AC⊥平面ABC₁.

∵AC⊂平面ABC，∴平面ABC⊥平面ABC₁，且交线是AB.故平面ABC₁上一点C₁在底面ABC的射影H必在交线AB上．

2．设a、b是不同的直线，α、β是不同的平面，则下列四个命题中正确的是(　)

A．若a⊥b，a⊥α，则b∥α

B．若a∥α，α⊥β，则a⊥β

C．若a⊥β，α⊥β，则a∥α

D．若a⊥b，a⊥α，b⊥β，则α⊥β

解析：选D.A中，b可能在α 内；B中，a可能在β内，也可能与β平行或相交(不垂直)；C中，a可能在α内；D中，a⊥b，a⊥α，则b⊂α或b∥α，又b⊥β，∴α⊥β.

1．若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中为真命题的是(　)

A．若m⊂β，α⊥β，则m⊥α

B．若α∩γ＝m，β∩γ＝n，m∥n，则α∥β

C．若α⊥γ，α⊥β，则β∥γ

D．若m⊥β，m∥α，则α⊥β

解析：选D.对于选项D，若m∥α，则过直线m的平面与平面α相交得交线n，由线面平行的性质定理可得m∥n，又m⊥β，故n⊥β，且n⊂α，故由面面垂直的判定定理可得α⊥β.

6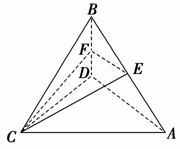．(2008年高考江苏卷)如图，在四面体ABCD中，CB＝CD，AD⊥BD，点E、F分别是AB、BD的中点，求证：

(1)直线EF∥平面ACD；

(2)平面EFC⊥平面BCD.

证明：(1)在△ABD中，因为E、F分别是AB、BD的中点，

所以EF∥AD.

又AD⊂平面ACD，EF⊄平面ACD，

所以直线EF∥平面ACD.

(2)在△ABD中，因为AD⊥BD，

EF∥AD，所以EF⊥BD.

在△BCD中，因为CD＝CB，F为BD的中点，

所以CF⊥BD.

因为EF⊂平面EFC，CF⊂平面EFC，

EF与CF交于点F，

所以BD⊥平面EFC.

又因为BD⊂平面BCD，

所以平面EFC⊥平面BCD.

练习

5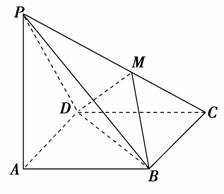．如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足__________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)

解析：由定理可知，BD⊥PC.

∴当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD，

而PC⊂平面PCD，∴平面MBD⊥平面PCD.

答案：DM⊥PC(或BM⊥PC等)

4.已知a、b是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：

①若a⊥α，a⊥β，则α∥β；

②若α⊥γ，β⊥γ，则α∥β；

③若α∥β，a⊂α，b⊂β，则a∥b；

④若α∥β，α∩γ＝a，β∩γ＝b，则a∥b.

其中正确命题的序号有________．

解析：垂直于同一直线的两平面平行，①正确；α⊥β也成立，②错；a、b也可异面，③错；由面面平行性质知，a∥b，④正确．

答案：①④

3．若l、m、n是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是(　)

A．若α∥β，l⊂α，n⊂β，则l∥n

B．若α⊥β，l⊂α，则l⊥β

C．若l⊥n，m⊥n，则l∥m

D．若l⊥α，l∥β，则α⊥β

解析：选D.选项A中，l除平行n外，还有异面的位置关系，则A不正确．选项B中，l与β的位置关系有相交、平行、在β内三种，则B不正确．选项C中，l与m的位置关系还有相交和异面，故C不正确．故选D.

2．设a、b、c表示三条直线，α、β表示两个平面，则下列命题的逆命题不成立的是(　)

A．c⊥α，若c⊥β，则α∥β

B．b⊂α，c⊄α，若c∥α，则b∥c

C．b⊂β，若b⊥α，则β⊥α

D．b⊂β，c是a在β内的射影，若b⊥c，则b⊥a

解析：选C.C选项的逆命题为b⊂β，若β⊥α则b⊥α.不正确，因为根据平面垂直的性质定理，如果两个平面垂直，其中一个平面内的直线只有垂直于交线的才垂直另一个平面．故选C.