3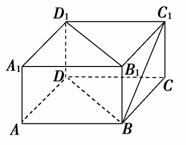．(2008年高考福建卷)如图，在长方体ABCD－A₁B₁C₁D₁中，AB＝BC＝2，AA₁＝1，则BC₁与平面BB₁D₁D所成角的正弦值为(　)

A.　　　　B.

C.　　　 　D.

解析：选D.以D点为坐标原点，以DA、DC、DD₁所在的直线为x轴、y轴、z轴，建立空间直角坐标系(图略)，

则A(2,0,0)，B(2,2,0)，C(0,2,0)，C₁(0,2,1)

∴＝(－2,0,1)，＝(－2,2,0)，且为平面BB₁D₁D的一个法向量．

∴cos〈，〉＝＝＝.

∴BC₁与平面BB₁D₁D所成角的正弦值为.

2．(原创题)如果平面的一条斜线和它在这个平面上的射影的方向向量分别是a＝(0,2,1)，b＝(，，)，那么这条斜线与平面的夹角是(　)

A．90°　 　　　　　　　　B．60°

C．45°　 　　　　　　　　D．30°

解析：选D.cosθ＝＝，因此a与b的夹角为30°.

1．设平面α的法向量为(1,2，－2)，平面β的法向量为(－2，－4，k)，若α∥β，则k＝(　)

A．2　　　　　B．－4

C．4　 　　　　　　　　　D．－2

解析：选C.∵α∥β，∴(－2，－4，k)＝λ(1,2，－2)，∴－2＝λ，k＝－2λ，∴k＝4.

12.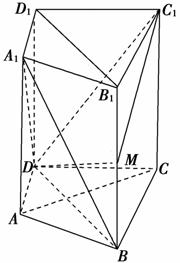如图所示，在直四棱柱ABCD-A₁B₁C₁D₁中，DB=BC，DB⊥AC，点M是棱BB₁上一点．

(1)求证：B₁D₁∥面A₁BD；

(2)求证：MD⊥AC；

(3)试确定点M的位置，使得平面DMC₁⊥平面CC₁D₁D.

解：(1)证明：由直四棱柱，得BB₁∥DD₁且BB₁＝DD₁，所以BB₁D₁D是平行四边形，

所以B₁D₁∥BD.

而BD⊂平面A₁BD，B₁D₁⊄平面A₁BD，

所以B₁D₁∥平面A₁BD.

(2)证明：因为BB₁⊥面ABCD，AC⊂面ABCD，所以BB₁⊥AC，

又因为BD⊥AC，且BD∩BB₁＝B，

所以AC⊥面BB₁D，

而MD⊂面BB₁D，所以MD⊥AC.

(3)当点M为棱BB₁的中点时，平面DMC₁⊥平面CC₁D₁D

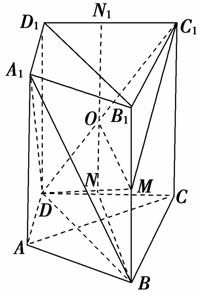
取DC的中点N，D₁C₁的中点N₁，连结NN₁交DC₁于O，连结OM.

因为N是DC中点，BD＝BC，所以BN⊥DC；又因为DC是面ABCD与面DCC₁D₁的交线，而面ABCD⊥面DCC₁D₁，

所以BN⊥面DCC₁D₁.

又可证得，O是NN₁的中点，所以BM∥ON且BM＝ON，即BMON是平行四边形，所以BN∥OM，所以OM⊥平面CC₁D₁D，因为OM⊂面DMC₁，所以平面DMC₁⊥平面CC₁D₁D.

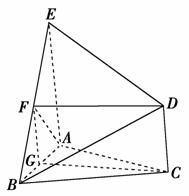
11.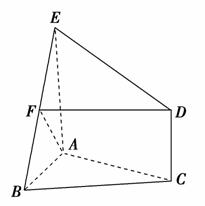如图所示，△ABC是正三角形，AE和CD都垂直于平面ABC，且AE=AB=2a，CD=a，F是BE的中点．

(1)求证：DF∥平面ABC；

(2)求证：AF⊥BD.

证明：(1)取AB的中点G，连结FG，可得FG∥AE，FG＝AE，

又CD⊥平面ABC，AE⊥平面ABC，

∴CD∥AE，CD＝AE，

∴FG∥CD，FG＝CD，

∵FG⊥平面ABC，

∴四边形CDFG是矩形，DF∥CG，

CG⊂平面ABC，DF⊄平面ABC，

∴DF∥平面ABC.

(2)Rt△ABE中，AE＝2a，AB＝2a，

F为BE中点，∴AF⊥BE，

∵△ABC是正三角形，∴CG⊥AB，

∴DF⊥AB，

又DF⊥FG，

∴DF⊥平面ABE，DF⊥AF，

∴AF⊥平面BDF，∴AF⊥BD.

10.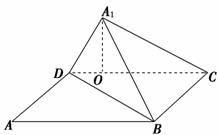(2010年南京模拟)如图，已知矩形ABCD中，AB=10，BC=6，沿矩形的对角线BD把△ABD折起，使A移到A₁点，且A₁在平面BCD上的射影O恰好在CD上．

求证：(1)BC⊥A₁D；

(2)平面A₁BC⊥平面A₁BD.

证明：(1)由于A₁在平面BCD上的射影O在CD上，

则A₁O⊥平面BCD，又BC⊂平面BCD，

则BC⊥A₁O，

又BC⊥CO，A₁O∩CO＝O，

则BC⊥平面A₁CD，又A₁D⊂平面A₁CD，

故BC⊥A₁D.

(2)因为ABCD为矩形，所以A₁B⊥A₁D.

由(1)知BC⊥A₁D，A₁B∩BC＝B，则A₁D⊥平面A₁BC，又A₁D⊂平面A₁BD.

从而有平面A₁BC⊥平面A₁BD.

9.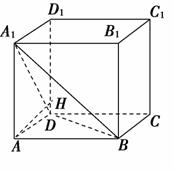如图所示，正方体ABCD-A₁B₁C₁D₁的棱长是1，过A点作平面A₁BD的垂线，垂足为点H，有下列三个命题：

①点H是△A₁BD的中心；

②AH垂直于平面CB₁D₁；

③AC₁与B₁C所成的角是90°.

其中正确命题的序号是　　　.

解析：由于ABCD-A₁B₁C₁D₁是正方体，所以A-A₁BD是一个正三棱锥，因此A点在平面A₁BD上的射影H是三角形A₁BD的中心，故①正确；又因为平面CB₁D₁与平面A₁BD平行，所以AH⊥平面CB₁D₁，故②正确；从而可得AC₁⊥平面CB₁D₁，即AC₁与B₁C垂直，所成的角等于90°.

答案：①②③

8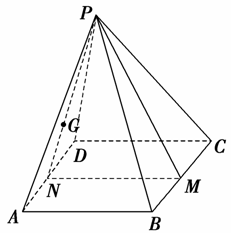．在正四棱锥P－ABCD中，PA＝AB，M是BC的中点，G是△PAD的重心，则在平面PAD中经过G点且与直线PM垂直的直线有________条．

解析：设正四棱锥的底面边长为a，则侧棱长为a.

由PM⊥BC，

∴PM＝ ＝a.

连结PG并延长与AD相交于N点，

则PN＝a，MN＝AB＝a，

∴PM²+PN²＝MN²，

∴PM⊥PN，又PM⊥AD，

∴PM⊥面PAD，

∴在平面PAD中经过G点的任意一条直线都与PM垂直．

答案：无数

7．已知m，n是直线，α、β、γ是平面，给出下列命题：

①α⊥γ，β⊥γ，则α∥β；

②若n⊥α，n⊥β，则α∥β；

③若n⊄α，m⊄α且n∥β，m∥β，则α∥β；

④若m，n为异面直线，n⊂α，n∥β，m⊂β，m∥α，则α∥β.

则其中正确的命题是_______．(把你认为正确的命题序号都填上)

解析：依题意可构造正方体ABCD-A₁B₁C₁D₁，如图所示，在正方体中逐一判断各命题易得正确的命题是②④.

答案：②④

6.在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，下面四个结论中不成立的是(　)

A．BC∥平面PDF

B．DF⊥平面PAE

C．平面PDF⊥平面ABC

D．平面PAE⊥平面ABC

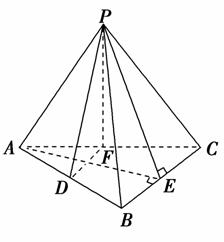解析：选C.

如图，∵BC∥DF，

∴BC∥平面PDF.∴A正确．

由题设知BC⊥PE，BC⊥AE，

∴BC⊥平面PAE.

∴DF⊥平面PAE.∴B正确．

∴平面ABC⊥平面PAE(BC⊥平面PAE)．∴D正确．