3.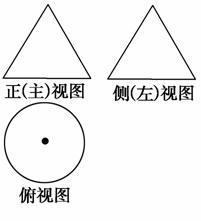一个几何体的三视图如图所示，其中正视图与侧视图都是边长为2的正三角形，则这个几何体的侧面积为(　)

A.π 　　　　　　　　B．2π

C．3π 　　　　　　　　D．4π

解析：选B.由三视图可知几何体为一圆锥，其中圆锥底面半径为1，母线长为2，故其侧面积S＝(2π×1)×2＝2π(其侧面展开图为一扇形，扇形半径为2，弧长为圆锥底面圆周长)，故选B.

2.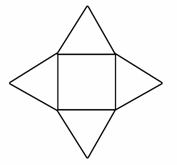如图，已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成，则该多面体的体积是(　)

A. 　　　　　　　　B.

C.　 　　　　　　　　　D.

解析：选B.由题知该多面体为正四棱锥，底面边长为1，侧棱长为1，斜高为，连结顶点和底面中心即为高，可得高为，所以体积为V＝·1·1·＝.

1．圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是(　)

A.π 　　　　　　　　　　　B．2π

C.π 　　　　　　　　　　　D.π

解析：选D.S₁＝π，S₂＝4π，∴r＝1，R＝2，

S＝6π＝π(r+R)l，∴l＝2，∴h＝.

∴V＝π(1+4+2)×＝π.

6．已知正方体AC₁的棱长为a，E、F分别为棱AA₁与CC₁的中点，求四棱锥A₁－EBFD₁的体积．

解：因为EB＝BF＝FD₁＝D₁E＝＝a，所以四棱锥A₁－EBFD₁的底面是菱形，连结EF，则△EFB≌△EFD₁，由于三棱锥A₁－EFB与三棱锥A₁－EFD₁等底同高，所以V_A1－EBFD1＝2V_A1－EFB＝2V_F－EBA1＝2··S_△EBA1·a＝a³.

练习

5．四边形ABCD中，A(0,0)，B(1,0)，C(2,1)，D(0,3)，绕y轴旋转一周，则所得旋转体的体积为________．

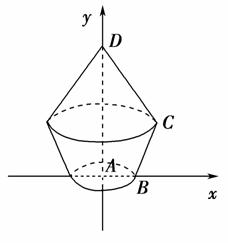
解析：V_圆锥＝πr²h＝π×2²×2

＝π，

V_圆台＝πh(r²+R²+Rr)

＝π×1×(2²+1²+2×1)＝π，

∴V＝V_圆锥+V_圆台＝5π.

答案：5π

4．(2009年高考全国卷Ⅰ)已知OA为球O的半径，过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π，则球O的表面积等于__________．

解析：由题意得圆M的半径r＝，设球的半径为R，又球心到圆M的距离为，由勾股定理得R²＝r²+()²，∴R＝2，则球的表面积为4π×2²＝16π，故填16π.

答案：16π

3．(原创题)设计一个杯子，其三视图如图所示，现在向杯中匀速注水，杯中水面的高度h随时间t变化的图象是(　)

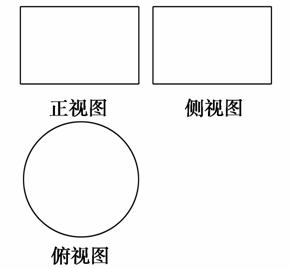
解析：选B.由三视图可知杯子是圆柱形的，由于圆柱形的杯子上下大小相同，所以当向杯中匀速注水时，其高度随时间的变化是相同的，反映在图象上，选项B符合题意．故选B.

2.已知A、B为球面上的两点，O为球心，且AB＝3，∠AOB＝120°，则球的体积为(　)

A. 　　　　　　　　　　　　B．4π

C．36π 　　　　　　　　　　　D．32π

解析：选B.△AOB为等腰三角形，∠AOB＝120°，AB＝3，通过解三角形解出OA和OB，即OA＝OB＝R＝，从而求出球的体积4π，故选B.

1．如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积为(　)

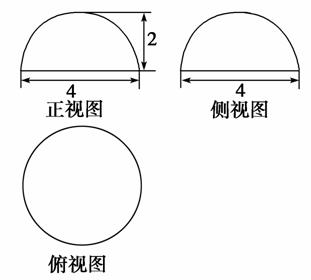
A．32π 　　　　　　　　　　　B．16π

C．12π　 　　　　　　　　　　　D．8π

解析：选C.由三视图可知几何体是半径为2的半球，故其表面积应为半球的表面积与底面圆的面积之和，即S＝2πR²+πR²＝3πR²＝12π.

4.长方体ABCD－A₁B₁C₁D₁中，AB＝AA₁＝2，AD＝1，E为CC₁的中点，则异面直线BC₁与AE所成角的余弦值为__________．

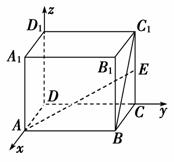解析：建立坐标系如图，

则A(1,0,0)，E(0,2,1)，

B(1,2,0)，C₁(0,2,2)，

＝(－1,0,2)，＝(－1,2,1)，

cos〈，〉＝＝.