1．以下四个命题中，正确命题的个数是(　)

①不共面的四点中，其中任意三点不共线；

②若点A、B、C、D共面，点A、B、C、E共面，则A、B、C、D、E共面；

③若直线a、b共面，直线a、c共面，则直线b、c共面；

④依次首尾相接的四条线段必共面．

A．0 　　　　　　　　　　　　　B．1

C．2 　　　　　　　　　　　　　D．3

解析：选B.①正确；②从条件看出两平面有三个公共点A、B、C，但是若A、B、C共线，则结论不正确；③不正确，共面不具有传递性；④不正确，因为此时所得的四边形四条边可以不在一个平面上．

12.一几何体按比例绘制的三视图如图所示(单位：m)：

(1)试画出它的直观图；

(2)求它的表面积和体积．

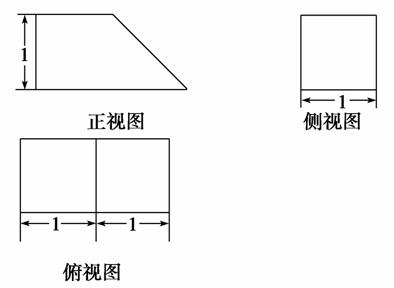
解：(1)直观图如图所示：

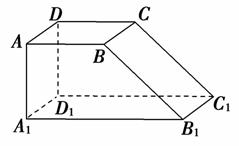
(2)法一：由三视图可知该几何体是长方体被截去一个角，且该几何体的体积是以A₁A，A₁D₁，A₁B₁为棱的长方体的体积的，

在直角梯形AA₁B₁B中，作BE⊥A₁B₁于E，则AA₁EB是正方形，

∴AA₁＝BE＝1.

在Rt△BEB₁中，BE＝1，EB₁＝1，

∴BB₁＝.

∴几何体的表面积S＝S_{正方形AA1D1D}+2S_梯形AA1B1B+S_矩形BB1C1C+S_{正方形ABCD}+S_{矩形A1B1C1D1}

＝1+2××(1+2)×1+1×+1+1×2

＝7+(m²)．

∴几何体的体积V＝×1×2×1＝(m³)，

∴该几何体的表面积为(7+)m²，体积为m³.

法二：几何体也可以看作是以AA₁B₁B为底面的直四棱柱，其表面积求法同法一，

V_{直四棱柱D1C1CD－A1B1BA}＝Sh

＝×(1+2)×1×1＝(m³)．

∴几何体的表面积为(7+)m²，体积为m³.

11．在底面直径和高均为2R的圆锥内作一内接圆柱，当圆柱的底面半径和高分别为多少时，它的体积最大？

解：如图，作出圆锥的轴截面，

设圆柱的高为h，

底面半径为r(0<r<R)，体积为V，

则＝，

∴h＝2(R－r)，

∴V＝πr²h＝2πr²(R－r)．

＝2πRr²－2πr³.

∴V′＝4πRr－6πr²，

由V′＝0得r＝R，

当r＝R时，圆柱的体积V取得最大值，

此时圆柱的高h＝2(R－R)＝R.

10．已知圆台的母线长为4 cm，母线与轴的夹角为30°，上底面半径是下底面半径的，求这个圆台的侧面积．

解：如图是将圆台还原为圆锥后的轴截面，

由题意知AC＝4 cm，∠ASO＝30°，

O₁C＝OA，

设O₁C＝r，则OA＝2r，

又＝＝sin30°，

∴SC＝2r，SA＝4r，

∴AC＝SA－SC＝2r＝4 (cm)，

∴r＝2 cm.

所以圆台的侧面积为S＝π(r+2r)×4＝24π(cm²)．

9.如图，在正三棱柱ABC-A₁B₁C₁中，D为棱AA₁的中点．若截面△BC₁D是面积为6的直角三角形，则此三棱柱的体积为　　　.

解析：设AC＝a，CC₁＝b，

则由(a²+b²)×2＝a²+b²，

得b²＝2a²，又×a²＝6，

∴a²＝8，∴V＝×8×4＝8.

答案：8

8.已知一个圆锥的展开图如图所示，其中扇形的圆心角为120°，底面圆的半径为1，则该圆锥的体积为　　　.

解析：因为扇形弧长为2π，所以圆锥母线长为3，高为2，所求体积V＝×π×1²×2＝.

答案：π

7．正三棱台高为12 cm，上、下底面面积之比为1∶4，它的体积为28 cm³，则下底面面积为__________．

解析：设下底面面积为S cm²，

则上底面面积为S cm²，

∴(S+S+ )×12＝28，

∴S＝4.

答案：4 cm²

6．把由曲线y＝|x|和y＝2围成的图形绕x轴旋转360°，所得旋转体的体积为(　)

A.　　　　　　　　　 　B.

C.　 　　　　　　　　　　D.

解析：选D.由题意，y＝|x|和y＝2围成图中阴影部分的图形，旋转体为一个圆柱挖去两个相同的共顶点的圆锥．

∵V_圆柱＝π·2²·4＝16π，

2V_圆锥＝2×π×2²×2＝，

∴所求几何体体积为16π－＝.

5.(2009年高考陕西卷)若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为(　)

A. 　　　　　　　　　　B.

C. 　　　　　　　　　　D.

解析：选B.所求八面体体积是两个底面边长为1，高为的四棱锥的体积和，一个四棱锥体积V₁＝×1×＝，故八面体体积V＝2V₁＝.故选B.

4．三棱锥P－ABC的四个顶点都在体积为的球的表面上，底面ABC所在的小圆面积为16π，则该三棱锥的高的最大值为(　)

A．7 　　　　　　　　　　B．7.5

C．8 　　　　　　　　　　D．9

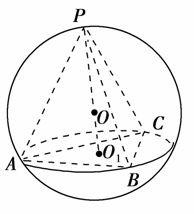解析：选C.设球的半径为R，πR³＝π，R＝5.设小圆半径为r，πr²＝16π，∴r＝4.当三棱锥的高过球心O时，取得最大值，OO₁＝＝3，PO₁＝5+3＝8.故选C.