3．已知函数f(x)＝x³+bx²+cx+d在区间[－1,2]上是减函数，那么b+c(　)

A．有最大值　 　　　　B．有最大值－

C．有最小值　 　　　　D．有最小值－

解析：选B.由f(x)在[－1,2]上是减函数，知

f′(x)＝3x²+2bx+c≤0，x∈[－1,2]，

则

⇒15+2b+2c≤0⇒b+c≤－.

2．(2010年佛山高中质检)若函数y＝x³+x²+mx+1是R上的单调函数，则实数m的取值范围是(　)

A．(，+∞)　 　　　　　B．(－∞，]

C．[，+∞)　 　　　　　D．(－∞，)

解析：选C.若函数y＝x³+x²+mx+1是R上的单调函数，只需y′＝3x²+2x+m≥0恒成立，即Δ＝4－12m≤0，∴m≥.故选C.

1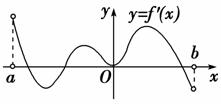．(原创题)函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内有极小值点的个数为(　)

A．1　　　　　 B．2

C．3　 　　　　　　　　　D．4

解析：选A.从f′(x)的图象可知f(x)在(a，b)内从左到右的单调性依次为增→减→增→减，∴在(a，b)内只有一个极小值点．

12.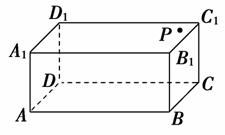在长方体ABCD－A₁B₁C₁D₁的面A₁C₁上有一点P(如图所示，其中P点不在对角线B₁D₁上)．

(1)过P点在空间中作一直线l，使l∥直线BD，应该如何作图？并说明理由；

(2)过P点在平面A₁C₁内作一直线m，使m与直线BD成α角，其中α∈(0，]，这样的直线有几条，应该如何作图？

解：(1)连结B₁D₁，在平面A₁C₁内过P作直线l，

使l∥B₁D₁，则l即为所求作的直线．

∵B₁D₁∥BD，l∥B₁D₁，∴l∥直线BD.

(2)在平面A₁C₁内作直线m，

使直线m与B₁D₁相交成α角，

∵BD∥B₁D₁，∴直线m与直线BD也成α角，

即直线m为所求作的直线．

由图知m与BD是异面直线，

且m与BD所成的角α∈(0，]．

当α＝时，这样的直线m有且只有一条，

当α≠时，这样的直线m有两条．

11.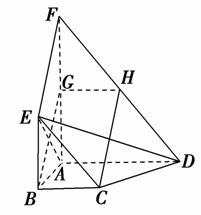 如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD＝∠FAB＝90°，BC綊AD，BE綊FA，G、H分别为FA、FD的中点．

　(1)证明：四边形BCHG是平行四边形；

(2)C、D、F、E四点是否共面？为什么？

解：(1)证明：由题设知，FG＝GA，FH＝HD，

所以GH綊AD.

又BC綊AD，故GH綊BC.

所以四边形BCHG是平行四边形．

(2)C、D、F、E四点共面．理由如下：

由BE綊AF，G是FA的中点知，BE綊GF，所以EF∥BG.

由(1)知BG∥CH，所以EF∥CH，故EC、FH共面．又点D在直线FH上，所以C、D、F、E四点共面．

10.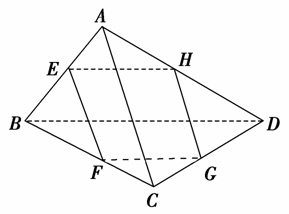如图所示，空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA上的点，请回答下列问题：

(1)满足什么条件时，四边形EFGH为平行四边形？

(2)满足什么条件时，四边形EFGH为矩形？

(3)满足什么条件时，四边形EFGH为正方形？

解：(1)当E，F，G，H分别为所在边的中点时，四边形EFGH为平行四边形，证明如下：

∵E，H分别是AB，AD的中点，

∴EH綊BD，同理，FG綊BD.

从而EH綊FG，所以四边形EFGH为平行四边形．

(2)当E，F，G，H分别为所在边的中点且BD⊥AC时，四边形EFGH为矩形．

(3)当E，F，G，H分别为所在边的中点且BD⊥AC，AC＝BD时，四边形EFGH为正方形．

9．空间四边形ABCD中，各边长均为1，若BD＝1，则AC的取值范围是__________．

解析：如图①所示，△ABD与△BCD均为边长为1的正三角形，当△ABD与△CBD重合时，AC＝0，将△ABD以BD为轴转动，到A，B，C，D四点再共面时，AC＝，如图②，故AC的取值范围是0<AC<.

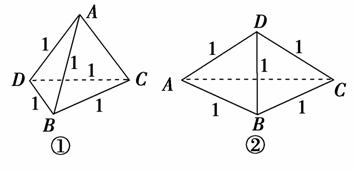
答案：(0，)

8.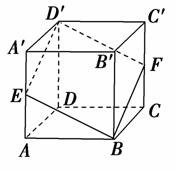在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则

①四边形BFD′E一定是平行四边形；

②四边形BFD′E有可能是正方形；

③四边形BFD′E在底面ABCD内的投影一定是正方形；

④平面BFD′E有可能垂直于平面BB′D.

以上结论正确的为　　　.(写出所有正确结论的编号)

解析：由平行平面的性质可得①，当E、F为棱中点时，四边形为菱形，但不可能为正方形．③④显然正确．

答案：①③④

7.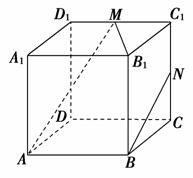如图，正方体ABCD-A₁B₁C₁D₁中，M、N分别为棱C₁D₁、C₁C的中点，有以下四个结论：

①直线AM与CC₁是相交直线；

②直线AM与BN是平行直线；

③直线BN与MB₁是异面直线；

④直线AM与DD₁是异面直线．

其中正确的结论为　　　(注：把你认为正确的结论的序号都填上)．

解析：直线AM与CC₁是异面直线，直线AM与BN也是异面直线，故①②错误．

答案：③④

6．正方体ABCD－A₁B₁C₁D₁，E，F分别是AA₁，CC₁的中点，P是CC₁上的动点(包括端点)，过点E、D、P作正方体的截面，若截面为四边形，则P的轨迹是(　)

A．线段C₁F 　　　　　　　　B．线段CF

C．线段CF和一点C₁　 　　　　D．线段C₁F和一点C

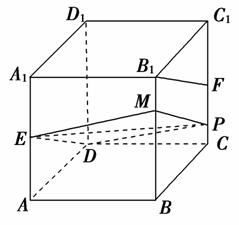解析：选C.如图，

DE∥平面BB₁C₁C，

∴平面DEP与平面BB₁C₁C的交线PM∥ED，连结EM，

易证MP=ED，

∴MP綊ED，则M到达B₁时仍可构成四边形，即P到F.而P在C₁F之间，不满足要求．P到点C₁仍可构成四边形．