7．f(x)＝x(x－c)²在x＝2处有极大值，则常数c的值为________．

解析：f(x)＝x³－2cx²+c²x，f′(x)＝3x²－4cx+c²，

f′(2)＝0⇒c＝2或c＝6，若c＝2，f′(x)＝3x²－8x+4，

令f′(x)>0⇒x<或x>2，f′(x)<0⇒<x<2，

故函数在(－∞，)及(2，+∞)上单调递增，在(，2)上单调递减，∴x＝2是极小值点，故c＝2不合题意，所以c＝6.

答案：6

6．设f(x)、g(x)是R上的可导函数，f′(x)，g′(x)分别为f(x)、g(x)的导函数，且满足f′(x)g(x)+f(x)g′(x)<0，则当a<x<b时，有(　)

A．f(x)g(b)>f(b)g(x) 　　　　　　B．f(x)g(a)>f(a)g(x)

C．f(x)g(x)>f(b)g(b)　 　　　　　　D．f(x)g(x)>f(b)g(a)

解析：选C.令y＝f(x)·g(x)，

则y′＝f′(x)·g(x)+f(x)·g′(x)，

由于f′(x)g(x)+f(x)g′(x)<0，

所以y在R上单调递减，

又x<b，故f(x)g(x)>f(b)g(b)．

5．已知函数y＝f(x)(x∈R)的图象如图所示，则不等式xf′(x)<0的解集为(　)

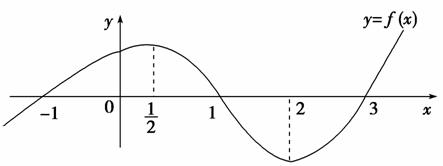
A．(-∞，)∪(,2)　 　　　　　　B．(－∞，0)∪(，2)

C．(－∞，∪(，+∞)　 　　　　D．(－∞，)∪(2，+∞)

解析：选B.由f(x)图象单调性可得f′(x)在(－∞，)∪(2，+∞)大于0，在(，2)上小于0，∴xf′(x)<0的解集为(－∞，0)∪(，2)．

4.函数f(x)＝e^x(sinx+cosx)在区间[0，]上的值域为(　)

A．[，e]　 　　　　　　　B．(，e)

C．[1，e]　 　　　　　　　　D．(1，e)

解析：选A.f′(x)＝e^x(sinx+cosx)+e^x(cosx－sinx)＝e^xcosx，

当0≤x≤时，f′(x)≥0，

∴f(x)是[0，]上的增函数．

∴f(x)的最大值为f()＝e，

f(x)的最小值为f(0)＝.

3．已知函数f(x)的导数为f′(x)＝4x³－4x，且f(x)的图象过点(0，－5)，当函数f(x)取得极大值－5时，x的值应为(　)

A．－1　 　　　　　　　　　　B．0

C．1　 　　　　　　　　　　　D．±1

解析：选B.可以求出f(x)＝x⁴－2x²+c，其中c为常数．

由于f(x)过(0，－5)，所以c＝－5，又由f′(x)＝0，得极值点为x＝0和x＝±1.又x＝0时，f(x)＝－5.故x的值为0.

2．函数f(x)＝x³－6b²x+3b在(0,1)内有极小值，则(　)

A．b＞0　 　　　　　　　　B．b＜

C．0＜b＜ 　　　　　　　D．b＜1

解析：选C.f′(x)＝3x²－6b²，令f′(x)＝0，得x＝±b.

∵f(x)在(0,1)内有极小值，

∴0＜b＜1.

∴0＜b＜.

1．已知f(x)的定义域为R，f(x)的导函数f′(x)的图象如图所示，则(　)

A．f(x)在x＝1处取得极小值

B．f(x)在x＝1处取得极大值

C．f(x)是R上的增函数

D．f(x)是(－∞，1)上的减函数，(1，+∞)上的增函数

解析：选C.由图象易知f′(x)≥0在R上恒成立，所以f(x)在R上是增函数．

6．(2009年高考北京卷)设函数f(x)＝x³－3ax+b(a≠0)．

(1)若曲线y＝f(x)在点(2，f(2))处与直线y＝8相切，求a，b的值；

(2)求函数f(x)的单调区间与极值点．

解：(1)f′(x)＝3x²－3a，

因为曲线y＝f(x)在点(2，f(2))处与直线y＝8相切，

所以即

解得a＝4，b＝24.

(2)f′(x)＝3(x²－a)(a≠0)．

当a<0时，f′(x)>0，函数f(x)在(－∞，+∞)上单调递增；此时函数f(x)没有极值点．

当a>0时，由f′(x)＝0得x＝±.

当x∈(－∞，－)时，f′(x)>0，函数f(x)单调递增；

当x∈(－，)时，f′(x)<0，函数f(x)单调递减．

当x∈(，+∞)时，f′(x)>0，函数f(x)单调递增．

此时x＝－是f(x)的极大值点，x＝是f(x)的极小值点．

练习

5．已知函数f(x)＝alnx+x在区间[2,3]上单调递增，则实数a的取值范围是________．

解析：∵f(x)＝alnx+x，∴f′(x)＝+1.

又∵f(x)在[2,3]上单调递增，

∴+1≥0在x∈[2,3]上恒成立，

∴a≥(－x)_max＝－2，∴a∈[－2，+∞)．

答案：[－2，+∞)

4．函数y＝3x²－6lnx的单调增区间为________，单调减区间为________．

解析：y′＝6x－＝.

∵定义域为(0，+∞)，由y′>0得x>1，

∴增区间为(1，+∞)；

由y′<0得0<x<1.

∴减区间为(0,1)．

答案：(1，+∞)　(0,1)