9．与直线3x+4y+12＝0平行，且与坐标轴构成的三角形的面积是24的直线l的方程是____________________．

解析：设直线l的方程为3x+4y＝a(a≠0)，

则直线l与两坐标轴的交点分别为(，0)，(0，)，

∴×||·||＝24，解得a＝±24，

∴直线l的方程为3x+4y＝±24.

答案：3x+4y+24＝0或3x+4y－24＝0

8．从点(2,3)射出的光线沿与直线x－2y＝0平行的直线射到y轴上，则经y轴反射的光线所在的直线方程为________________．

解析：由题意得，射出的光线方程为y－3＝(x－2)，即x－2y+4＝0，与y轴交点为(0,2)，

又(2,3)关于y轴对称点为(－2,3)，

∴反射光线所在直线过(0,2)，(－2,3)，

故方程为y－2＝x，即x+2y－4＝0.

答案：x+2y－4＝0

7．已知a＝(6,2)，b＝(－4，)，直线l过点A(3，－1)，且与向量a+2b垂直，则直线l的一般方程是____________________．

解析：a+2b＝(－2,3)，设P(x，y)为直线l上任意一点，由(a+2b)⊥，得直线l的一般方程是2x－3y－9＝0.

答案：2x－3y－9＝0

6．设点A(－2,3)，B(3,2)，若直线ax+y+2＝0与线段AB没有交点，则a的取值范围是(　)

A．(－∞，－]∪[，+∞) 　　　　B．(－，)

C．[－，] 　　　　　　　　　　D．(－∞，－]∪[，+∞)

解析：选B.直线ax+y+2＝0恒过点M(0，－2)，

且斜率为－a，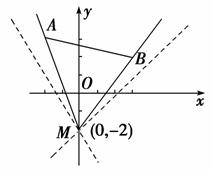

∵k_MA＝＝－，

k_MB＝＝，

由图可知：－a＞－且－a＜，

∴a∈(－，)，故选B.

5.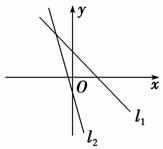已知直线l₁，l₂的方程分别为x+ay+b＝0，x+cy+d＝0，其图象如图所示，则有(　)

A．ac＜0 　　　　　　B．a＜c

C．bd＜0　 　　　　　D．b＞d

解析：选C.直线方程化为

l₁：y＝－x－，l₂：y＝－x－.

由图象知，－＜－＜0，－＞0＞－，

∴a＞c＞0，b＜0，d＞0.

4．若点A(a,0)，B(0，b)，C(1，－1)(a＞0，b＜0)三点共线，则a－b的最小值等于(　)

A．4 　　　　　　　　　　　　B．2

C．1　 　　　　　　　　　　　D．0

解析：选A.∵A、B、C三点共线，

∴k_AB＝k_AC，即＝，∴－＝1，

∴a－b＝(a－b)(－)＝2－－

＝2+[(－)+(－)]≥2+2＝4.

(当a＝－b＝2时取等号)

3．若直线(2m²+m－3)x+(m²－m)y＝4m－1在x轴上的截距为1，则实数m是(　)

A．1 　　　　　　　　　　　B．2

C．－　 　　　　　　　　　　D．2或－

解析：选D.当2m²+m－3≠0时，

在x轴上截距为＝1，即2m²－3m－2＝0，

∴m＝2或m＝－.

2．直线2xcosα－y－3＝0(α∈[，])的倾斜角的变化范围是(　)

A．[，] 　　　　　　　　　B.　 [，]

C．[，)　 　　　　　　　　　D．[，]

解析：选B.直线2xcosα－y－3＝0的斜率k＝2cosα，由于α∈[，]，所以≤cosα≤，因此k＝2cosα∈[1，]．设直线的倾斜角为θ，则有tanθ∈[1，]，由于θ∈[0，π)，

所以θ∈[，]，即倾斜角的变化范围是[，]．

1．与直线x+4y－4＝0垂直，且与抛物线y＝2x²相切的直线方程为(　)

A．4x－y+1＝0　　　　B．4x－y－1＝0

C．4x－y－2＝0　　　　　　 　D．4x－y+2＝0

答案：C

6．△ABC的三个顶点为A(－3,0)，B(2,1)，C(－2,3)，求：

(1)BC所在直线的方程；

(2)BC边上中线AD所在直线的方程；

(3)BC边上的垂直平分线DE的方程．

解：(1)因为直线BC经过B(2,1)和C(－2,3)两点，由两点式得BC的方程为＝，即x+2y－4＝0.

(2)设BC中点D的坐标为(x，y)，则

x＝＝0，y＝＝2.

BC边的中线AD过点A(－3,0)，D(0,2)两点，由截距式得AD所在直线方程为+＝1，即2x－3y+6＝0.

(3)BC的斜率k₁＝－，则BC的垂直平分线DE的斜率k₂＝2，由斜截式得直线DE的方程为y＝2x+2.

练习