1．如果在测量中，某渠道斜坡的坡度为，设α为坡角，那么cosα等于(　)

A.　 　　　　　　　　　　　　B.

C. 　　　　　　　　　　　　　D.

解析：选B.因tanα＝，所以cosα＝.

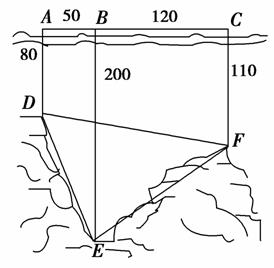
6．(2009年高考宁夏海南卷)如图，为了解某海域海底构造，在海平面内一条直线上的A、B、C三点进行测量．已知AB＝50 m，BC＝120 m，于A处测得水深AD＝80 m，于B处测得水深BE＝200 m，于C处测得水深CF＝110 m，求∠DEF的余弦值．

解：如图作DM∥AC交BE于N，交CF于M.

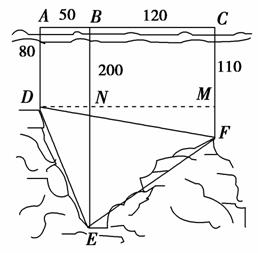
解：如图作DM∥AC交BE于N，交CF于M.

DF＝＝＝10(m)，

DE＝＝＝130(m)，

EF＝＝＝150(m)．

在△DEF中，由余弦定理的变形公式，得

cos∠DEF＝＝＝.

练习

5.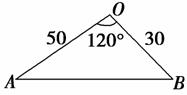轮船A和轮船B在中午12时同时离开海港O，两船航行方向的夹角为120°，两船的航行速度分别为25 n mile/h、15 n mile/h，则下午2时两船之间的距离是________n mile.

解析：如图，由题意可得OA＝50，OB＝30.

而AB²＝OA²+OB²－2OA·OBcos120°

＝50²+30²－2×50×30×(－)

＝2500+900+1500＝4900，

∴AB＝70.

答案：70

4．在△ABC中，设命题p：＝＝；命题q：△ABC是等边三角形．那么命题p是命题q的________条件．

解析：命题p：＝＝.由正弦定理＝＝，得sinA＝sinB＝sinC，

∴A＝B＝C⇒a＝b＝c.反之，亦成立．

答案：充分必要

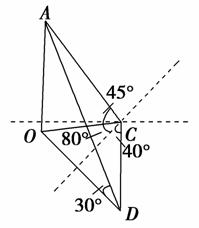
3．某人在C点测得塔顶A为南偏西80°，仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，则塔高为(　)

A．15米 　　　　　　　　　　B．5米

C．10米　 　　　　　　　　　　D．12米

解析：选C.如图，设塔高为h，

在Rt△AOC中，∠ACO＝45°，

则OC＝OA＝h.

在Rt△AOD中，

∠ADO＝30°，则OD＝h，

在△OCD中，

∠OCD＝120°，CD＝10，

由余弦定理得：OD²＝OC²+CD²－2OC·CDcos∠OCD，

即(h)²＝h²+10²－2h×10×cos120°，

∴h²－5h－50＝0，解得h＝10或h＝－5(舍)．

2．在△ABC中，B＝45°，C＝60°，c＝1，则最短边的边长是(　)

A.　 　　　　　　　　　　　B.

C.　 　　　　　　　　　　　　D.

解析：选A.由＝，得b＝＝＝，

∵B角最小，∴最短边是b.

1．(2010年江南十校质检)在三角形ABC中，A＝120°，AB＝5，BC＝7，则的值为(　)

A.　 　　　　　　　　　　　　B.

C.　 　　　　　　　　　　　　D.

解析：选A.由余弦定理可得25+AC²－10AC·cos120°＝49⇒AC＝3，由正弦定理得＝＝，故选A.

12．已知直线l与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线l的方程：(1)过定点A(－3,4)；(2)斜率为.

解：(1)设直线l的方程是y＝k(x+3)+4，

它在x轴、y轴上的截距分别是－－3,3k+4，

由已知，得|(3k+4)(－－3)|＝6，

解得k₁＝－或k₂＝－.

所以直线l的方程为

2x+3y－6＝0或8x+3y+12＝0.

(2)设直线l在y轴上的截距为b，

则直线l的方程是y＝x+b，它在x轴上的截距是－6b，

由已知，得|－6b·b|＝6，∴b＝±1.

∴直线l的方程为x－6y+6＝0或x－6y－6＝0.

11.在△ABC中，已知A(5，－2)、B(7,3)，且AC边的中点M在y轴上，BC边的中点N在x轴上，求：

(1)顶点C的坐标；

(2)直线MN的方程．

解：(1)设C(x，y)，M(0，b)，N(a,0)，

则，解得x＝－5，y＝－3，a＝1，b＝－.

∴C(－5，－3)．

(2)由(1)知M(0，－)，N(1,0)，

∴k_MN＝，∴MN的方程为y＝(x－1)，

即5x－2y－5＝0.

10．(1)求经过点A(－5,2)且在x轴上的截距等于在y轴上的截距的2倍的直线方程．

(2)过点A(8,6)引三条直线l₁，l₂，l₃，它们的倾斜角之比为1∶2∶4，若直线l₂的方程是y＝x，求直线l₁，l₃的方程．

解：(1) ①当横截距、纵截距都为零时，设所求的直线方程为y＝kx，将(－5,2)代入y＝kx中，得k＝－，此时，直线方程为y＝－x，即2x+5y＝0.

②当横截距、纵截距都不是零时，设所求直线方程为+＝1，

将(－5,2)代入所设方程，

解得a＝－，

此时，直线方程为x+2y+1＝0.

综上所述，所求直线方程为

x+2y+1＝0或2x+5y＝0.

(2)设直线l₂的倾斜角为α，则tanα＝.

于是tan ＝＝＝，

tan2α＝＝＝，

所以所求直线l₁的方程为y－6＝(x－8)，

即x－3y+10＝0，

l₃的方程为y－6＝(x－8)，

即24x－7y－150＝0.