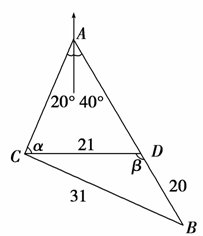
11．某观测站在城A南偏西20°方向的C处，由城A出发的一条公路，走向是南偏东40°，在C处测得公路距C 31千米的B处有一人正沿公路向城A走去，走了20千米后到达D处，此时CD间的距离为21千米，问这人还要走多少千米可到达城A?

解：如图所示，设∠ACD=α，∠CDB=β.在△CBD中．由余弦定理得

cosβ＝

＝＝－，

∴sinβ＝.

而sinα＝sin(β－60°)

＝sinβcos60°－sin60°cosβ

＝·+·＝.

在△ACD中，＝，

∴AD＝＝15(千米)．

所以这人再走15千米才可到城A.

10．(2009年高考山东卷)已知函数f(x)＝2sinxcos²+cosxsinφ－sinx(0<φ<π)在x＝π处取最小值．

(1)求φ的值；

(2)在△ABC中，a，b，c分别是角A，B，C的对边，已知a＝1，b＝，f(A)＝，求角C.

解：(1)f(x)＝2sinx+cosxsinφ－sinx

＝sinx+sinxcosφ+cosxsinφ－sinx

＝sinxcosφ+cosxsinφ

＝sin(x+φ)．

因为f(x)在x＝π时取最小值，

所以sin(π+φ)＝－1，故sinφ＝1.

又0<φ<π，所以φ＝.

(2)由(1)知f(x)＝sin(x+)＝cosx.

因为f(A)＝cosA＝，

且A为△ABC的内角，所以A＝.

由正弦定理得sinB＝＝，

又b>a，所以B＝或B＝.

当B＝时，C＝π－A－B＝π－－＝，

当B＝时，C＝π－A－B＝π－－＝.

综上所述，C＝或C＝.

9．一船以每小时15 km的速度向东航行，船在A处看到一灯塔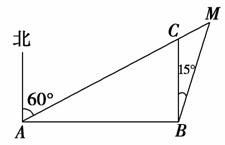M在北偏东60°方向，行驶4 h后，船到达B处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为________km.

解析：如图，依题意有

AB＝15×4＝60，

∠MAB＝30°，∠AMB＝45°，

在△AMB中，

由正弦定理得＝，

解得BM＝30(km)．

答案：30

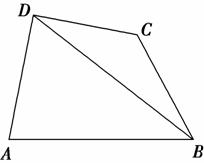
8．如图，在四边形ABCD中，已知AD⊥CD，AD＝10，AB＝14，∠BDA＝60°，∠BCD＝135°，则BC的长为________．

解析：在△ABD中，设BD＝x，则BA²＝BD²+AD²－2BD·AD·cos∠BDA，即14²＝x²+10²－2·10x·cos60°，整理得x²－10x－96＝0，解之得x₁＝16，x₂＝－6(舍去)．

在△BCD中，由正弦定理：＝，

∴BC＝·sin30°＝8.

答案：8

7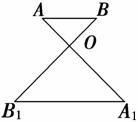．如图，AA₁与BB₁相交于点O，AB∥A₁B₁且AB＝A₁B₁.若△AOB的外接圆的直径为1，则△A₁OB₁的外接圆的直径为________．

解析：在△AOB中，由正弦定理得＝1，sin∠AOB＝AB，在△A₁OB₁中，由正弦定理得2R＝＝＝2.

答案：2

6.一船自西向东航行，上午10时到达灯塔P的南偏西75°、距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船航行的速度为(　)

A.海里/时　 　　　　　　　B．34海里/时

C.海里/时　 　　　　　　　D．34海里/时

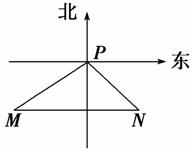解析：选A.如图，由题意知∠MPN＝75°+45°＝120°，∠PNM＝45°.

在△PMN中，由正弦定理，得

＝，

∴MN＝68×＝34.

又由M到N所用时间为 14－10＝4(小时)，

∴船的航行速度v＝＝(海里/时)．

5．如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救，甲船立即前往营救，同时把消息告知在甲船的南偏西30°，相距10海里C处的乙船，乙船立即朝北偏东θ角的方向沿直线前往B处救援，则sinθ的值等于(　)

A. 　　　　　　　　　　　B.

C. 　　　　　　　　　　　D.

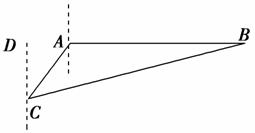解析：选D.根据题目条件可作图如图：在△ABC中，AB＝20，AC＝10，∠CAB＝120°，由余弦定理有

BC²＝AC²+AB²－2AC·ABcos∠CAB

＝20²+10²－2×20×10cos120°

＝700，

∴BC＝10，再由正弦定理得＝，

∴sin∠ACB＝＝＝，

cos∠ACB＝.

所以sinθ＝sin(30°+∠ACB)

＝sin30°cos∠ACB+cos30°sin∠ACB

＝×+×＝.

4．一船向正北航行，看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上，继续航行半小时后，看见一灯塔在船的南偏西60°，另一灯塔在船的南偏西75°，则这艘船的速度是每小时(　)

A．5海里　 　　　　　　　　　B．5海里

C．10海里　 　　　　　　　　D．10海里

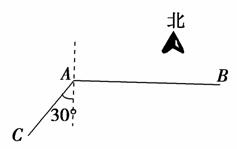
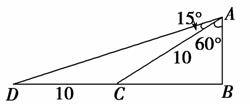解析：选C.如图，依题意有∠BAC=60°，∠BAD=75°，所以∠CAD=∠CDA=15°，从而CD=CA=10，在直角三角形ABC中，得AB=5，于是这艘船的速度是=10(海里/小时)．

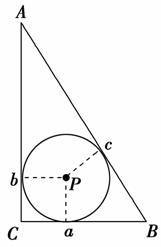
3．如图，若Rt△ABC的斜边AB＝2，内切圆的半径为r，则r的最大值为(　)

A.　 B．1

C.　 D.－1

解析：选D.∵r＝＝－1，

∵4＝a²+b²≥，

∴(a+b)²≤8.∴a+b≤2，∴r≤－1.故选D.

2．在△ABC中，角A，B均为锐角，且cosA>sinB，则△ABC的形状是(　)

A．直角三角形　 　　　　　　B．锐角三角形

C．钝角三角形　 　　　　　　D．等腰三角形

解析：选C.cosA＝sin(－A)>sinB，－A，B都是锐角，则－A>B，A+B<，C>.