295. 已知空间不共面的四个点，与此四个点距离都相等的平面有________个．

解析：与不共面的四个点距离相等的平面分为两类，一类是四个点中一个点位于平面的一侧，另外三个点在平面的另一侧，这样的平面有4个；另一类是四个点中的两个点位于平面一侧，另外两个点在平面的另一侧，这样的平面有3个，故一共7个平面到这四个点距离相等．

294. 已知AC，BD是夹在两平行平面a 、b 间的线段，A∈a ，B∈a ，C∈b ，D∈b ，且AC=25cm，BD=30cm，AC、BD在平面b 内的射影的和为25cm，则AC、BD在平面b 内的射影长分别为________，AC与平面b 所成的角的正切值为________，BD与平面b 所成的角的正切值为________．

解析：设a 、b 间的距离为h，AC在平面b 内的射影，BD在平面b 内的射影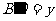，根据已知条件可得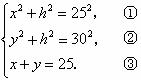②-①得，即

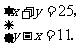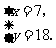，把③代入得y-x=11，∴　 解得即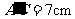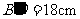，．又h=24cm，AC与平面b 所成的角为，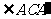

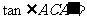
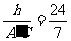，同理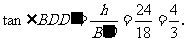

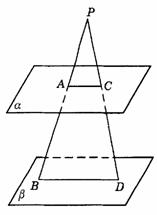
293. 平面a ∥平面b ，过平面a 、b 外一点P引直线PAB分别交a 、b 于A、B两点，PA=6，AB=2，引直线PCD分别交a 、b 于C、D两点．已知BD=12，则AC的长等于(　)．

　A．10　　　　B．9　　　　C．8　　　　D．7

解析：B．如图答9-32，平面PBD∩a =AC，平面PBD∩b =BD，∵　a ∥b ，∴　AC∥BD．由平面几何知识知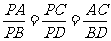，．∵　PA=6，AB=2，BD=12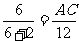，∴　，∴　AC=9．

292. 设a 、b 是两个平面，l和m是两条直线，那么a ∥b 的一个充分条件是(　)．

　A．l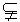a ，m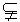a ，且l∥b ，m∥b 　　B．l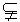a ，mb ，且l∥m

　C．l⊥a ，m⊥b ，且l∥m　　　　 D．l∥a ，m∥b ，且l∥m

解析：C．可参看图答9-31．

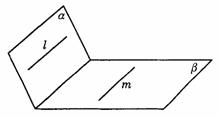
图答9-31

291. 给出下列命题，错误的命题是(　)．

　A．若直线a平面a ，且a ∥平面b ，则直线a与平面b 的距离等于平面a 、b 间的距离

　B．若平面a ∥平面b ，点A∈a ，则点A到平面b 的距离等于平面a 、b 间的距离

　C．两条平行直线分别在两个平行平面内，则这两条直线间的距离等于这两个平行平面间的距离

　D．两条异面直线分别在两个平行平面内，则这两条直线间的距离等于这两个平行平面间的距离

解析：C．以下按顺序说明，对A中，在a上任取一点P，作PH⊥b ，PH为直线a与平面b 的距离．∵　a ∥b ，PH⊥a ，∴　PH又为a 、b 间的距离．对于B，作AH⊥b ，AH的长为点A到b 的距离．又∵　a ∥b ，∴　AH⊥a ，于是AH的长是a 、b 两个平行平面间的距离．

　对于C，设a∥b，a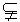a ，b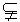b ，过a上任一点P作PQ⊥b于Q，则PQ的长为a、b两平行直线间的距离．因为PQ与a 、b 不一定垂直，所以PQ的长一般不是a 、b 间的距离，一般地说，a、b间的距离不小于a 、b 间的距离．

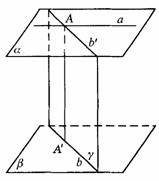
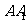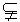　对于D．设是异面直线a、b的公垂线段，A∈a，，aa ，b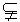b ，过A和b的平面与a 相交于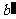，则，于是．∴　．同理 ．故的长又是a 、b 两个平面间的距离(如图答9-30)．　

4．定义运算ab＝ab²+a²b，则sin15°cos15°的值是________．

解析：依题意，可知

sin15°cos15°＝sin15°cos²15°+sin²15°cos15°

＝sin30°sin(15°+45°)＝.

3．已知α，β，γ∈(0，)，且sinα+sinγ＝sinβ，cosβ+cosγ＝cosα，则α－β的值等于(　)

A.　 　　　　　　　　　B．－

C．±　 　　　　　　　　D．±

解析：选B.sinβ－sinα＝sinγ＞0，cosα－cosβ＝cosγ＞0，则(sinβ－sinα)²+(cosα－cosβ)²＝1，且β＞α，即cos(α－β)＝(0＜α＜β＜)，则α－β＝－，故选B.

2.·等于(　)

A．tanα　 　　　　　　　B．tan2α

C．1　 　　　　　　　　D.

解析：选B.原式＝·＝＝tan2α.

1．已知cos2α＝，则sin²α＝(　)

A.　 　　　　　　　　　B.

C.　 　　　　　　　　　D.

解析：选D.cos2α＝1－2sin²α，∴＝1－2sin²α，

∴sin²α＝，故选D.

12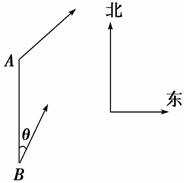．如图所示，甲船由A岛出发向北偏东45°的方向作匀速直线航行，速度为15海里/小时，在甲船从A岛出发的同时，乙船从A岛正南40海里处的B岛出发，朝北偏东θ(tanθ＝)的方向作匀速直线航行，速度为10海里/小时．

(1)求出发后3小时两船相距多少海里？

(2)求两船出发后多长时间距离最近？最近距离为多少海里？

(3)两船在航行中能否相遇，试说明理由．

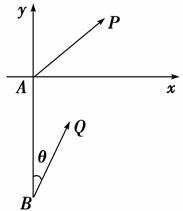解：以A为原点，BA所在直线为y轴建立如图所示的平面直角坐标系．

设在t时刻甲、乙两船分别在P(x₁，y₁)、Q(x₂，y₂)处．

则

由tanθ＝可得，

cosθ＝，sinθ＝，

故

(1)令t＝3，P、Q两点的坐标分别为(45,45)，(30,20)，

|PQ|＝＝＝5.

即出发后3小时两船相距5海里．

(2)由(1)的解法过程易知：

|PQ|＝

＝

＝＝≥20，

∴当且仅当t＝4时，|PQ|取得最小值20.

即两船出发4小时后距离最近，最近距离为20海里．

(3)由(2)可知，两船之间的最近距离为20海里，所以两船在航行中不会相遇