
题目列表(包括答案和解析)
133. 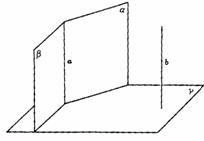 已知:平面α∩平面β=直线a.
已知:平面α∩平面β=直线a.
α,β同垂直于平面γ,又同平行于直线b.
求证:(Ⅰ)a⊥γ;
(Ⅱ)b⊥γ.
证明:
证法一(Ⅰ)设α∩γ=AB,β∩γ=AC.在γ内任取一点P并于γ内作直线PM⊥AB,PN⊥AC. --1分
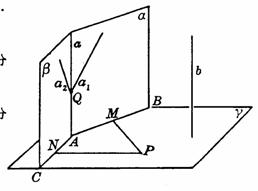 ∵ γ⊥α,
∵ γ⊥α,
∴ PM⊥α.
而 a α,
α,
∴ PM⊥a.
同理PN⊥a. --4分
又 PM γ,PN
γ,PN γ,
γ,
∴ a⊥γ. --6分
(Ⅱ)于a上任取点Q,过b与Q作一平面交α于直线a1,交β于直线a2. --7分
∵ b∥α,∴ b∥a1.
同理b∥a2. --8分
∵ a1,a2同过Q且平行于b,
∵ a1,a2重合.
又 a1 α,a2
α,a2 β,
β,
∴ a1,a2都是α、β的交线,即都重合于a. --10分
∵ b∥a1,∴ b∥a.
而a⊥γ,
∴ b⊥γ. --12分
注:在第Ⅱ部分未证明b∥a而直接断定b⊥γ的,该部分不给分.
证法二(Ⅰ)在a上任取一点P,过P作直线a′⊥γ. --1分
∵ α⊥γ,P∈α,
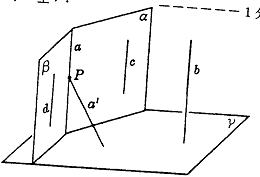 ∴ a′
∴ a′ α.
α.
同理a′ β.
--3分
β.
--3分
可见a′是α,β的交线.
因而a′重合于a. --5分
又 a′⊥γ,
∴ a⊥γ. --6分
(Ⅱ)于α内任取不在a上的一点,过b和该点作平面与α交于直线c.同法过b作平面与β交于直线d. --7分
∵ b∥α,b∥β.
∴ b∥c,b∥d. --8分
又 c β,d
β,d β,可见c与d不重合.因而c∥d.
β,可见c与d不重合.因而c∥d.
于是c∥β. --9分
∵ c∥β,c α,α∩β=a,
α,α∩β=a,
∴ c∥a. --10分
∵ b∥c,a∥c,b与a不重合(b α,a
α,a α),
α),
∴ b∥a. --11分
而 a⊥γ,
∴ b⊥γ. --12分
注:在第Ⅱ部分未证明b∥a而直接断定b⊥γ的,该部分不给分.
3、作斜线在平面内的射影, 只要在斜线上找一点作直线 垂直于平面, 即找此点在平面内的射影, 显然找V点, V点在平面内的射影在何处?由条件可知, 射影为△ABC的外心。
解: 作VO^平面ABC于O, 则OB为VB在平面ABC内的射影,
∴ÐVBO为VB与平面ABC所成的角。
连OA、OB、OC, 则OA、OB、OC分别为斜线段VA、VB、VC在平面ABC内的射影。
∵VA = VB = VC
∴OA = OB = OC
∴O为△ABC为外心
∵△ABC为直角三角形, 且AC为斜边
∴O为AC的中点
设VA = a, 则VA = VC = AC = a, 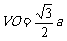
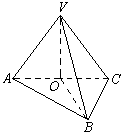
在Rt△VOB中, 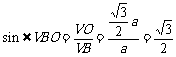
∴ÐVBO = 60°
∴VB与平面ABC所成的角为60°。
2、要作出VB与平面ABC所成的角, 只要找出VB在平 面ABC内的射影就可以了。
132. 如图: △ABC的ÐABC= 90°, V是平面ABC外的一点, VA = VB = VC = AC, 求VB与平面ABC所成的角。
解析:1、要求VB与平面ABC所成的角, 应作出它们所成的角。
131. 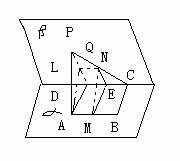 如图在二面角α- l-β中,A、B∈α,C、D∈l,ABCD为矩形,P∈β,PA⊥α,且PA=AD,MN依次是AB、PC的中点
如图在二面角α- l-β中,A、B∈α,C、D∈l,ABCD为矩形,P∈β,PA⊥α,且PA=AD,MN依次是AB、PC的中点
⑴ 求二面角α- l-β的大小
⑵ 求证明:MN⊥AB
⑶ 求异面直线PA与MN所成角的大小
解析:⑴ 用垂线法作二面角的平面角
⑵ 只要证明AB垂直于过MN的一个平面即可
⑶ 过点A作MN的平行线,转化为平面角求解
解:
⑴ 连PD
∵PA⊥α,AD⊥l
∴PD⊥l
∴∠PDA为二面角α- l-β的平面角
在RTΔPAD中
∵PA=PD
∴∠PDA=45°
∴二面角α- l-β为45°
⑵ 设E是DC的中点,连ME、NE
∵M、N、E分别为AB、PC、D的中点
∴ME∥AD,NE∥PD
∴ME⊥l,NE⊥l
∴l⊥平面MEN
∵AB∥l
∴AB⊥平面MEN
∵MNÌ平面MNE
∴MN^AB
⑶ 设Q是DP听中点,连NQ、AQ
则NQ∥DC,且NQ=1/2DC
∵AM∥DC,且AM=1/2AB=1/2DC
∴QN∥AM,QN=AM
∴QNMQ为平行四边形
∴AQ∥MN
∴∠PAQ为PA与MN所成的角
∵ΔPAQ为等腰直角三角形,AQ为斜边上的中线
∴∠PAQ=45°
即PA与MN所成角的大小为45°
300. 已知四面体A-BCD,AO1⊥平面BCD,且O1为ΔBCD的垂心.BO2⊥平面ACD,求证:O2是ΔACD的垂心.
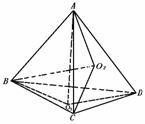
证明 如图所示,连结BO1,AO2,
∵AO1⊥平面BCD,O1为ΔBCD的垂心,
∴BO1⊥CD,由三垂线定理得AB⊥CD.
又BO2⊥平面ACD,由三垂线逆定理得AO2⊥CD.
同理连结DO1,CO2可证BC⊥AD,即CO2⊥AD.
∴O2是ΔACD垂心.
299. 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F
(1)求证:AF⊥SC
(2)若平面AEF交SD于G,求证:AG⊥SD
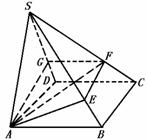
解析: 如图,欲证AF⊥SC,只需证SC垂直于AF所在平面,即SC⊥平面AEF,由已知,欲证SC⊥平面AEF,只需证AE垂直于SC所在平面,即AE⊥平面ABC,再由已知只需证AE⊥BC,而要证AE⊥BC,只需证BC⊥平面SAB,而这可由已知得证
证明 (1)∵SA⊥平面AC,BC 平面AC,∴SA⊥BC
平面AC,∴SA⊥BC
∵矩形ABCD,∴AB⊥BC
∴BC⊥平面SAB
∴BC⊥AE又SB⊥AE ∴AE⊥平面SBC
∴SC⊥平面AEF
∴AF⊥SC
(2)∵SA⊥平面AC ∴SA⊥DC,又AD⊥DC
∴DC⊥平面SAD ∴DC⊥AG
又由(1)有SC⊥平面AEF,AG 平面AEF
平面AEF
∴SC⊥AG ∴AG⊥平面SDC ∴AG⊥SD
298. 如图9-38,已知平面a ∥平面b ,A、C∈a ,B、D∈b ,E、F分别为AB、CD的中点.求证:EF∥a ,EF∥b .
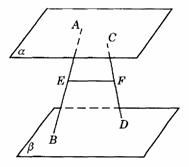
解析:当AB、CD共面时,平面ABCD∩a
=AC,平面ABCD∩b =BD.∵ a
∥b ,∴ AC∥BD.∵ E、F分别为AB、CD的中点,∴ EF∥AC.∵ AC
 a ,EF
a ,EF
 a ,∴ EF∥a
,同理EF∥b
.当AB、CD异面时,∵
a ,∴ EF∥a
,同理EF∥b
.当AB、CD异面时,∵ 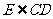 ,∴ 可在平面ECD内过点E作
,∴ 可在平面ECD内过点E作 ,与a ,b 分别交于
,与a ,b 分别交于 ,
, .平面
.平面 ,平面
,平面 ,∵ a ∥b ,∴
,∵ a ∥b ,∴  .∵ E是AB中点,∴ E也是
.∵ E是AB中点,∴ E也是 的中点.平面
的中点.平面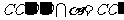 ,平面
,平面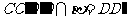 ,∵ a ∥b ,∴
,∵ a ∥b ,∴  ,∵ E、F分别为
,∵ E、F分别为 、CD中点,∴
、CD中点,∴ 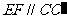 ,
,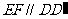 .∵
.∵ 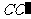
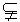 a ,EF
a ,EF
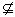 a ,∴ EF∥a
,同理EF∥b
.
a ,∴ EF∥a
,同理EF∥b
.
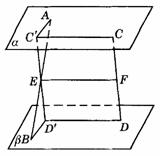
297. 如图9-37,两条异面直线AB、CD与三个平行平面a 、b 、g 分别相交于A、E、B,及C、F、D,又AD、BC与平面b 的交点为H、G.求证:EHFG为平行四边形.
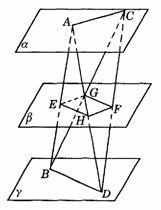 解析:
解析:
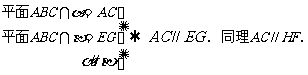
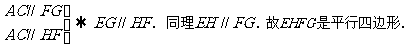
296.
如图9-35,平面a
∥平面b ,△ABC、△ 的分别在a 、b 内,线段
的分别在a 、b 内,线段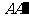 、
、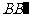 、
、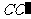 相交于点O,O在a 、b 之间.若AB=2,AC=1,∠ABC=60°,OA∶
相交于点O,O在a 、b 之间.若AB=2,AC=1,∠ABC=60°,OA∶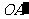 =3∶2,则△
=3∶2,则△ 的面积为________.
的面积为________.
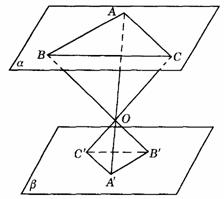
解析:图9-35
∵ 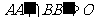 ,∴
,∴ 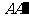 、
、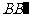 确定平面
确定平面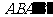 ,平面
,平面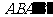 ∩a =AB,平面
∩a =AB,平面 ,∵ a ∥b ,∴
,∵ a ∥b ,∴ 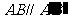 ,同理
,同理 ,
,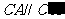 .由于方向相反,∴ △ABC与△
.由于方向相反,∴ △ABC与△ 的三内角相等,∴ △ABC∽△
的三内角相等,∴ △ABC∽△ .且
.且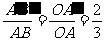 . ∵
. ∵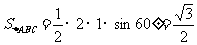 ,∴
,∴ 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com