
题目列表(包括答案和解析)
283.
平面a ∥平面b ,a a ,b
a ,b b ,则a、b一定是( ).
b ,则a、b一定是( ).
A.两条平行直线 B.异面直线
C.相交直线 D.无公共点的两条直线
解析:D.a ∥b ,则平面a 与b 无公共点,a、b一定无公共点.
282. 判断下列命题是否正确,并说明理由.
(1)若两个平面有无数个公共点,则这两个平面重合;
(2)在一个平面内有三条直线和另一个平面平行,那么这两个平面平行;
(3)若两个平面相交,那么分别在这两个平面内的两条直线也相交;
(4)如果两个平面平行,那么分别在这两个平面内的两条直线也平行;
(5)一条直线与两个平行平面所成的角相等;
(6)一条直线与两个平行平面中的一个平行,那么一定平行于另一个平面.
解析:(1)不正确.两个平面还可能相交于一条直线;
(2)不正确.两个平面可能相交,这三条直线均与交线平行;
(3)不正确.分别在两个相交平面内的两条直线也可能平行,它们都平行于交线;
(4)不正确.两条直线还可能异面;
(5)正确.无论直线与两个平面相对位置如何,直线与两个平面所成的角都相等;
(6)不正确.直线可能在另一个平面上.
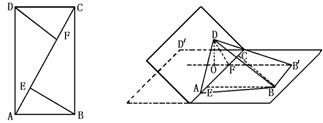
281. 如图,矩形ABCD中,AB=2,BC=2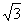 ,以AC为轴翻折半平面,使二平面角B-AC-D为120°,求:(1)翻折后,D到平面ABC的距离;(2)BD和AC所成的角.
,以AC为轴翻折半平面,使二平面角B-AC-D为120°,求:(1)翻折后,D到平面ABC的距离;(2)BD和AC所成的角.
解析:研究翻折问题,通常要画出翻折前的平面图形和翻折后的空间图形,对应点的字母要相同.
解 分别过B、D作AC的垂线,垂足是E、F,过F作FB′∥BE,过B作BB′∥AC,交点B′,则四边形EFB′B是矩形.
∵AC⊥DF,AC⊥B′F,∴AC⊥平面B′FD,即∠DF′B就是二面角B-AC-D的平面角,亦即∠DFB′=120°.
过D作DO⊥B′F,垂足为O.∵DO 平面DFB′,AC⊥平面DFB′.∴DO⊥AF,DO⊥平面ABC.
平面DFB′,AC⊥平面DFB′.∴DO⊥AF,DO⊥平面ABC.
在RtΔADC中,CD=2,AD=2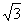 ,∴DF=
,∴DF=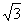 ,OD=DF·sin60°=
,OD=DF·sin60°=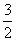 .
.
(2)在ΔDFB′中,DB′=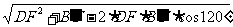 =3.
=3.
又由(1)可知,AC∥BB′,AC⊥平面DFB′⊥平面DFB′.∴BB′⊥平面DFB′,∴ΔDB B′是直角三角形,又BB′=EF=2.∴tan∠DBB′=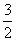 .
.
∵AC∥BB′,∴AC与BD所成的角就是∠DBB′,即为arctan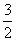 .
.
说明 处理翻折问题,只要过不在棱上的点作棱的垂直相交的线段,就可以化成基本题型处理,本题也可以这样考虑,即利用异面直线DF、BE上两点B、D间的距离,先求出BD2=EF2+DF2+BE2-2DF·BE·cos120°=13,从而得出∠DBB′=arccos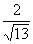 .
.
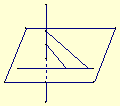
60. l1、l2是两条异面直线,直线m1、m2与l1、l2都相交,则m1、m2的位置关系是( )
A.异面或平行 B.相交
C.异面 D.相交或异面
解析:D
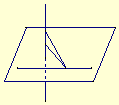
59. 垂直于同一条直线的两条直线的位置关系是( )
A.平行 B.相交
C.异面 D.以上都有可能
解析:D
58. 已知异面直线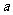 与
与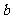 所成的角为
所成的角为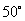 ,P为空间一定点,则过点P且与
,P为空间一定点,则过点P且与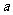 ,
,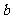 所成的角均是
所成的角均是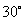 的直线有且只有( )
的直线有且只有( )
A、1条 B、2条 C、3条 D、4条
解析: 过空间一点P作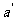 ∥
∥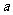 ,
,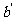 ∥
∥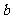 ,则由异面直线所成角的定义知:
,则由异面直线所成角的定义知: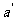 与
与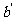 的交角为
的交角为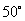 ,过P与
,过P与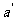 ,
,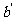 成等角的直线与
成等角的直线与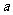 ,
,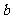 亦成等角,设
亦成等角,设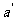 ,
,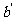 确定平面
确定平面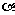 ,
,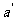 ,
,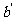 交角的平分线为
交角的平分线为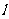 ,则过
,则过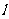 且与
且与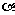 垂直的平面(设为
垂直的平面(设为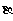 )内的任一直线
)内的任一直线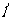 与
与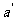 ,
,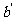 成等角(证明从略),由上述结论知:
成等角(证明从略),由上述结论知: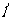 与
与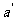 ,
,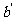 所成角大于或等于
所成角大于或等于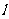 与
与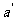 ,
,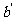 所成角
所成角 ,这样在
,这样在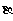 内
内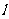 的两侧与
的两侧与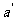 ,
,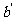 成
成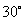 角的直线各有一条,共两条。在
角的直线各有一条,共两条。在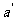 ,
,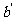 相交的另一个角
相交的另一个角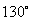 内,同样可以作过
内,同样可以作过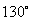 角平分线且与
角平分线且与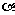 垂直的平面
垂直的平面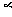 ,由上述结论知,
,由上述结论知,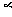 内任一直线与
内任一直线与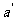 ,
,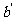 所成角大于或等于
所成角大于或等于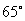 ,所以
,所以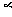 内没有符合要求的直线,因此过P与
内没有符合要求的直线,因此过P与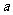 ,
,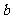 成
成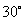 的直线有且只有2条,故选(B)
的直线有且只有2条,故选(B)
57. 三棱柱 ,平面
,平面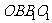 ⊥平面OAB,
⊥平面OAB,

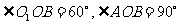 ,且
,且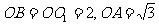 ,求异面直线
,求异面直线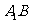 与
与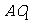 所成角的大小,(略去了该题的1问)
所成角的大小,(略去了该题的1问)
解析: 在平面 内作
内作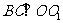 于C ,连
于C ,连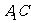 ,
,
由平面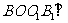 平面AOB,
平面AOB,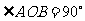 知,
知,
AO⊥平面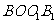 , ∴
, ∴ 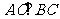 ,
,
又  , ∴ BC⊥平面
, ∴ BC⊥平面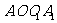 ,
,
∴ 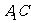 为
为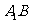 在平面
在平面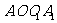 内的射影。
内的射影。
设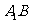 与
与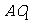 所成角为
所成角为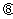 ,
,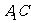 与
与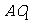 所成角为
所成角为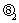 ,
,
则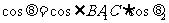 ,
,
由题意易求得 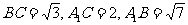 ,
,
∴ 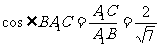 ,
,
在矩形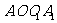 中易求得
中易求得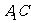 与
与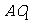 所成角
所成角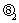 的余弦值:
的余弦值: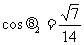 ,
,
∴ 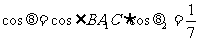 ,
,
即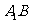 与
与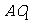 所成角为
所成角为 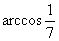 。
。
56.. 在正四面体ABCD中,E,F分别为BC,AD的中点,
求异面直线AE与CF所成角的大小。
解析: 连接BF、EF,易证AD⊥平面BFC,
∴ EF为AE在平面BFC内的射影,
设AE与CF所成角为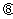 ,
,
 ∴
∴ 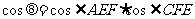 ,
,
设正四面体的棱长为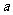 ,则
,则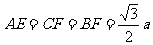 ,
,
显然 EF⊥BC, ∴ 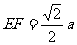 ,
,
∴ 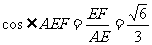 ,
, 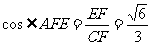 ,
,
∴ 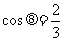 , 即AE∴与CF所成角为
, 即AE∴与CF所成角为 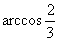 。
。
55. 已知平行六面体
已知平行六面体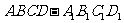 的底面ABCD是菱形,且
的底面ABCD是菱形,且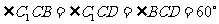 ,证明
,证明 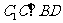 。
。
(略去了该题的2,3问)
解析: 设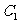 在平面ABCD内射影为H,则CH为
在平面ABCD内射影为H,则CH为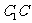 在平面ABCD内的射影,
在平面ABCD内的射影,
∴ 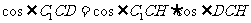 ,
,
∴ 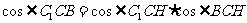 ,
,
由题意 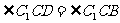 , ∴
, ∴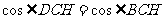 。
。
又 ∵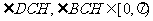
∴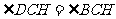 , 从而CH为
, 从而CH为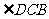 的平分线,
的平分线,
又四边形ABCD是菱形, ∴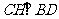
∴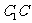 与BD所成角为
与BD所成角为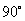 , 即
, 即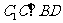
54. 已知AO是平面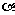 的斜线,A是斜足,OB垂直
的斜线,A是斜足,OB垂直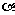 ,B为垂足,则
,B为垂足,则
直线AB是斜线在平面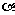 内的射影,设AC是
内的射影,设AC是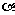 内的任一条直线,
内的任一条直线,
解析:设AO与AB所成角为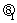 ,AB与AC所成角为
,AB与AC所成角为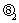 ,AO与AC所成角为
,AO与AC所成角为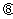 ,则有
,则有
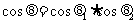 。
。
在三棱锥S-ABC中,∠SAB=∠SAC=
∠ACB=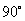 ,
,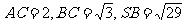 ,求异面直线SC与AB所成角的大小。(略去了该题的1,2问)
,求异面直线SC与AB所成角的大小。(略去了该题的1,2问)
 由SA⊥平面ABC知,AC为SC在平面ABC内的射影,
由SA⊥平面ABC知,AC为SC在平面ABC内的射影,
设异面直线SC与AB所成角为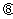 ,
,
则  ,
,
由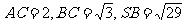 得
得
∴ 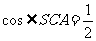 ,
, 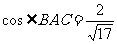 ,
,
∴ 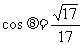 , 即异面直线SC与AB所成角为
, 即异面直线SC与AB所成角为 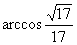 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com