
题目列表(包括答案和解析)
266. 正方体的两条体对角线所夹角的正弦值为______________。
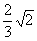
解析:易知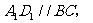 故
故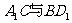 两条体对角线相交,设交点为O(如图),则
两条体对角线相交,设交点为O(如图),则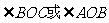 即为所成的角。
即为所成的角。
设正方体棱长为1,则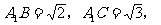
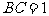 ,所以
,所以 ,而
,而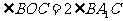 ,故
,故
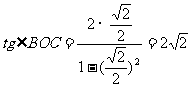 ,即
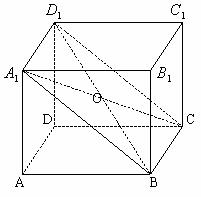
,即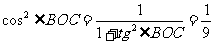 ,
,
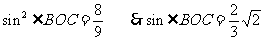
265.试证:两两相交且不全过同一点的四条直线共面.
解析:(1)设a、b、c、d四条直线两两相交,且不过同一点,并且无三线共点.
记 a∩b=A,a∩c=C,c∩b=B,
∵ a∩b=A,∴ a、b确定平面α.
∴ B∈b,C∈a. ∴ B、C∈α.
∴
BC α,即c
α,即c α,同理d
α,同理d α
α
从而 a、b、c、d共面
(2)若有三线共点,不妨设b、c、d相交于A,
a∩b=B,a∩c=C,a∩d=D.
∴ a与A可确定平面α.
∵
B∈a.
∴B∈α,于是b α.
α.
同理,c α,d
α,d α.
α.
从而a、b、c、d共面.
264.异面直线l1、l2,它们之间的距离为1,所成角是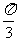 ,它们的公垂线是AB,A∈l1,B∈l2.E∈l1,F∈l2,AE=BF=1,求EF的长.
,它们的公垂线是AB,A∈l1,B∈l2.E∈l1,F∈l2,AE=BF=1,求EF的长.
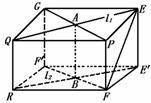
解析:如图,用异面直线l1、l2作为长方体的上、下底面的对角线,公垂线AB为高.
①EF的长即是正方形PEE′F的对角线长,为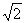 .
.
②侧面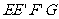 的对角线
的对角线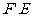 ,用勾股定理得
,用勾股定理得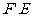 =2,即为所求.
=2,即为所求.
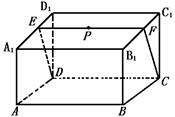
263. 在一块长方形木块的面上有一点P,木匠师傅要用锯子从P和CD将木块分成两块,问怎样画线.
解析:过P作C1D1的平行线EF,连DE、CF.
262.如果直线a垂直于直线b,那么直线a与平行于直线b的任意一条直线b′互相垂直
解析:在a上任取一点A,过A作b1∥b,则a与b1垂直.
∵b∥b′,b∥b1 ∴b1∥b′
∴直线a与b1和a与b′所成的角相等.
∴a⊥b′
261. 已知空间四边形ABCD,E、H分别是AB、AD的中点,F、G分别是边BC、DC的三等分点.
求证:①对角线AC、BD是异面直线,
②EF和HG必交于一点,且交点在AC上.
解析:①提示:用反证法,或者用判定定理.
②提示:先证EH∥FG,EH<FG,设FE∩GH=0
又
0∈GH.GH 平面ADC.∴O∈平面ADC.同理O∈平面ABC.
平面ADC.∴O∈平面ADC.同理O∈平面ABC.
∴O在平面ADC和平面ABC的交线AC上.
279. 在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°的角.(如图所示)
在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°的角.(如图所示)
(1)求点C′到平面AB′C的距离;(2)求二面角B-B′C-A的余弦值.
解析:(1)∵ABC-A′B′C′是直三棱柱,∴A′C′∥AC,AC 平面AB′C,∴A′C′∥平面AB′C,于是C′到平面AB′C的距离等于点A′到平面AB′C的距离,作A′M⊥AB′于M.由AC⊥平面AB′A′得平面AB′C⊥平面AB′A′,∴A′M⊥平面AB′C,A′M的长是A′到平面AB′C的距离.
平面AB′C,∴A′C′∥平面AB′C,于是C′到平面AB′C的距离等于点A′到平面AB′C的距离,作A′M⊥AB′于M.由AC⊥平面AB′A′得平面AB′C⊥平面AB′A′,∴A′M⊥平面AB′C,A′M的长是A′到平面AB′C的距离.
∵AB=B′B=1,⊥B′CB=30°,∴B′C=2,BC=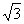 ,AB′=
,AB′= ,A′M=
,A′M=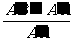 =
=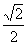 .即C′到平面AB′C的距离为
.即C′到平面AB′C的距离为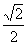 ;
;
(2)作AN⊥BC于N,则AN⊥平面B′BCC′,作NQ⊥B′C于Q,则AQ⊥B′C,∴∠AQN是所求二面角的平面角,AN=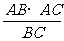 =
=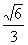 ,AQ=
,AQ=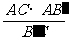 =1.∴sin∠AQN=
=1.∴sin∠AQN= =
=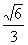 ,cos∠AQN=
,cos∠AQN=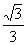 .
.
说明 利用异面直线上两点间的距离公式,也可以求二面角的大小,如图,AB=BB′=1,∴AB′= ,又∠B′CB=30°,
,又∠B′CB=30°,
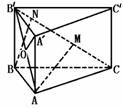 ∴BC=
∴BC=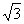 ,B′C=2,AC=
,B′C=2,AC= .作AM⊥B′C于M,BN⊥B′C于N,则AM=1,BN=
.作AM⊥B′C于M,BN⊥B′C于N,则AM=1,BN=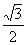 ,
,
CN=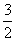 ,CM=1,∴MN=
,CM=1,∴MN=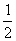 .∵BN⊥B′C,AM⊥B′C,∴BN与AM所成的角等于二面角B-B′C-A的平面角.设为θ.由AB2=AM2+BN2+MN2-2AM×BN×cosθ得cosθ=
.∵BN⊥B′C,AM⊥B′C,∴BN与AM所成的角等于二面角B-B′C-A的平面角.设为θ.由AB2=AM2+BN2+MN2-2AM×BN×cosθ得cosθ=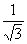 =
=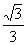 .
.
280 如图所示,四棱锥P-ABCD的底面是边长为a的菱形,∠A=60°,PC⊥平面ABCD,PC=a,E是PA的中点.
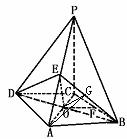 (1)求证平面BDE⊥平面ABCD.(2)求点E到平面PBC的距离.(3)求二面角A-EB-D的平面角大小.
(1)求证平面BDE⊥平面ABCD.(2)求点E到平面PBC的距离.(3)求二面角A-EB-D的平面角大小.
解析:(1)设O是AC,BD的交点,连结EO.
∵ABCD是菱形,∴O是AC、BD的中点,
∵E是PA的中点,∴EO∥PC,又PC⊥平面ABCD,
∴EO⊥平面ABCD,EO 平面BDE,∴平面BDE⊥平面ABCD.
平面BDE,∴平面BDE⊥平面ABCD.
(2)EO∥PC,PC 平面PBC,
平面PBC,
∴EO∥平面PBC,于是点O到平面PBC的距离等于E到平面PBC的距离.
作OF⊥BC于F,
∵EO⊥平面ABCD,EO∥PC,PC 平面PBC,∴平面PBC⊥平面ABCD,于是OF⊥平面PBC,OF的长等于O到平面PBC的距离.
平面PBC,∴平面PBC⊥平面ABCD,于是OF⊥平面PBC,OF的长等于O到平面PBC的距离.
由条件可知,OB=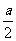 ,OF=
,OF=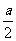 ×
×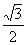 =
=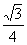 a,则点E到平面PBC的距离为
a,则点E到平面PBC的距离为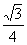 a.
a.
(3)过O作OG⊥EB于G,连接AG ∵OE⊥AC,BD⊥AC ∴AC⊥平面BDE
∴AG⊥EB(三垂线定理) ∴∠AGO是二面角A-EB-D的平面角
∵OE=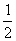 PC=
PC=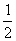 a,OB=
a,OB=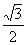 a ∴EB=a.∴OG=
a ∴EB=a.∴OG=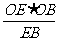 =
=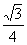 a 又AO=
a 又AO=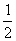 a.
a.
∴tan∠AGO=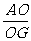 =
=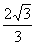 ∴∠AGO=arctan
∴∠AGO=arctan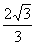 .
.
评析 本题考查了面面垂直判定与性质,以及利用其性质求点到面距离,及二面角的求法,三垂线定理及逆定理的应用.
278.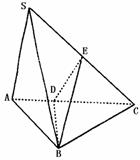 如图所示,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图所示,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
解法一:由于SB=BC,且E是SC中点,因此BE是等腰三角形SBC的底边SC的中线,所以SC⊥BE.又已知SC⊥DE,BE∩DE=E,
∴SC⊥平面BDE,∴SC⊥BD,
又∵SA⊥底面ABC,BD在底面ABC上,∴SA⊥BD.
而SA∩SC=S,所以BD⊥平面SAC.
∵DE=平面SAC∩平面BDE,DC=平面SAC∩平面BDC,
∴BD⊥DE,BD⊥DC.∴∠EDC是所求二面角的平面角.
∵SA⊥底面ABC,∴SA⊥AB,SA⊥AC.
设SA=a,则AB=a,BC=SB= a.
a.
又AB⊥BC,所以AC=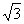 a.在RtΔSAC中tg∠ACS=
a.在RtΔSAC中tg∠ACS=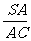 =
=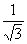 ,所以∠ACS=30°.
,所以∠ACS=30°.
又已知DE⊥SC,所以∠EDC=60°,即所求的二面角等于60°.
解法二:由于SB=BC,且E是SC的中点,因此BE是等腰ΔSBC的底边SC的中线,所以SC⊥BE.又已知SC⊥DE,BE∩DE=E.∴SC⊥平面BDE,SC⊥BD.
由于SA⊥底面ABC,且A是垂足,所以,AC是SC在平面ABC上的射影,由三垂线定理的逆定理得BD⊥AC;又E∈SC,AC是SC在平面内的射影,所以E在平面ABC内的射影在AC上,由于D∈AC,所以DE在平面ABC内的射影在AC上,根据三垂线定理得BD⊥DE.
∵DE 平面BDE,DC
平面BDE,DC 平面BDC.∴∠EDC是所求二面角的平面角.以下解法同解法一.
平面BDC.∴∠EDC是所求二面角的平面角.以下解法同解法一.
277.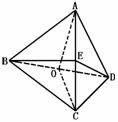 如图,四面体ABCD的棱BD长为2,其余各棱的长均是
如图,四面体ABCD的棱BD长为2,其余各棱的长均是 ,求:二面角A-BD-C、A-BC-D、B-AC-D的大小.
,求:二面角A-BD-C、A-BC-D、B-AC-D的大小.
解析:(1)取BD的中点O,连AO、OC.在ΔABD中,∵AB=AD= ,BD=2,
,BD=2,
∴ΔABD是等腰直角三角形,AO⊥BD,同理OC⊥BD.
∴∠AOC是二面角A-BD-C的平面角
又AO=OC=1,AC= ,∴∠AOC=90°.即二面角A-BD-C为直二面角.
,∴∠AOC=90°.即二面角A-BD-C为直二面角.
(2)∵二面角A-BD-C是直二面角,AO⊥BD,∴AO⊥平面BCD.
∴ΔABC在平面BCD内的射影是ΔBOC.
∵SΔOCB=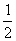 ,SΔABC=
,SΔABC=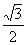 ,∴cosθ=
,∴cosθ=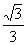 .即二面角A-BC-D的大小是arccos
.即二面角A-BC-D的大小是arccos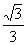 .
.
(3)取AC的中点E,连BE、DE.∵AB=BC,AD=DC,
∴BD⊥AC,DE⊥AC,∴∠BED就是二面角的平面角.
在ΔBDE中,BE=DE=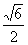 ,由余弦定理,得cosα=-
,由余弦定理,得cosα=-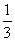
∴二面角B-AC-D的大小是π-arccos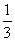 .
.
评析 本例提供了求二面角大小的方法:先作出二面角的平面角,再利用其所在的三角形算出角的三角函数值,或利用面积的射影公式S′=S·cosθ求得.
276. 在三棱锥S-ABC中,∠ASB=∠BSC=60°,∠ASC=90°,且SA=SB=SC,求证:平面ASC⊥平面ABC.
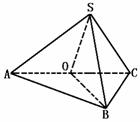 证明 取AC的中点O,连SO、BO,由已知,得ΔSAB、ΔSBC都是正三角形.∴BC=AB=a,SA=SC=a,又SO⊥AC,BO⊥AC,∴∠SOB就是二面角S-AC-B的平面角.又∵SA=AB=a,SC=BC=a,AC=AC,∴ΔACS≌ΔACB.
证明 取AC的中点O,连SO、BO,由已知,得ΔSAB、ΔSBC都是正三角形.∴BC=AB=a,SA=SC=a,又SO⊥AC,BO⊥AC,∴∠SOB就是二面角S-AC-B的平面角.又∵SA=AB=a,SC=BC=a,AC=AC,∴ΔACS≌ΔACB.
∴SO=BO=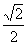 a.在ΔSOB中,∵SB=a,∴∠SOB=90°.
a.在ΔSOB中,∵SB=a,∴∠SOB=90°.
即平面SAC⊥平面ABC.
另证:过S作SO⊥平面ABC,垂足是O.∵SA=SB=SC,∴S在平面内的射影是ΔABC的外心,同前面的证明,可知ΔABC是直角三角形,∴O在斜边AC上.又∵平面SAC经过SO,∴平面SAC⊥平面ABC
说明 证明“面面垂直”的常用方法是根据定义证明平面角是90°,或利用判定定理证明一个平面经过另一个平面的垂线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com