230. 判断题：正确的在括号内打“√”号，不正确的打“×”号

229.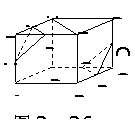如图：在正方体ABCD－EFGH中，M、N、P、Q、R、S分别是AE、EH、EF、CG、BC、CD的中点，求证：平面MNP//平面QRS。 解析：先证明SR//BD，BD//HF,HF//NP, ∴SR//平面MNP,再证RO//平面MNP， 从而证明平面MNP//平面QRS

228. 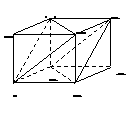如图：在正方体ABCD－EFGH中，求证：平面AFH//平面BDG。 解析：易证BD//平面AHF，BG//平面AHF， ∴平面BDG//平面AHF。

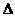227.如图2－24：B为ACD所在平面外一点，M、N、G分别为ABC、ABD、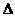BCD的重心， (1)求证：平面MNG//平面ACD； (2)求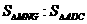

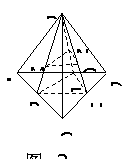解析：(1)要证明平面MNG//平面ACD，由于M、N、G分别 为△ABC、△ABD、△BCD的重心，因此可想到利用重心的性 质找出与平面平行的直线。

证明:连结BM、BN、BG并延长交AC、AD、CD分别于P、F、H。 ∵M、N、G分别为△ABC、△ABD、△BCD的重心， 则有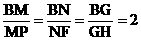： 连结PF、FH、PH有MN∥PF，又PF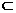平面ACD，∴MN∥平面ACD。 同理：MG∥平面ACD，MG∩MN＝M， ∴平面MNG∥平面ACD

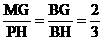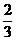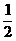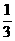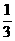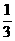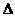(2)分析：因为△MNG所在的平面与△ACD所在的平面相互平行，因此，求两三角形的面积之比，实则求这两个三角形的对应边之比。 解：由(1)可知， ∴MG＝PH，又PH＝AD，∴MG＝AD 同理：NG＝AC，MN＝CD， ∴MNG∽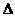ACD，其相似比为1：3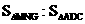， ∴＝1：9

点评:立体几何问题，一般都是化成平面几何问题，所以要重视平面几何。比如重心定理，三角形的三边中线交点叫做三角形有重心，到顶点的距离等于它到对边中点距离的2倍。

226. 如图2－23：已知正方体ABCD－A₁B₁C₁D₁，求证：平面AB₁D₁//平面BDC₁。

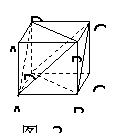解析：要证明两个平面平行，由面面平行的判定定理知，须在某一平面内寻找两条相交且与另一平面平行的直线

证明:∵AB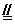C₁D₁，C₁D₁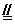A₁B₁，∴AD₁//BC₁∴AB 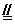A₁B₁， ∴四边形ABC₁D₁为平行四边形，又AD₁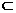平面AB₁D₁，BC₁平面AB₁D₁，∴BC₁//平面AB₁D₁，同理，BD//平面AB₁D₁，又BD∩BC₁＝B， ∴平面AB₁D₁//平面BDC₁。

点评:证面面平行，通常转化为证线面平行，而证线面平行又转化为证线线平行，所以关键是证线线平行。

225.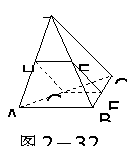如图2－32：平面EFGH分别平行于CD、AB，E、F、G、H分别在BD、BC、AC、AD上，且CD＝a，AB＝b，CD⊥AB (1)求证：EFGH是矩形

(2)点E在什么位置时，EFGH的面积最大

(1)证明：∵CD//平面EFGH，而平面EFGH∩平面BCD＝EF ∴CD//EF，同理HG//CD，∴EF// HG，同理HE//GF， ∴四边形EFGH为平行四边形，由CD//EF，HE// AB， ∴∠HEF为CD和AB所成的角 又∵CD⊥AB，∴HE⊥EF ∴四边形EFGH为矩形 (2)解：由(1)可知在BCD中EF//CD，设DE＝m，EB＝n

224. 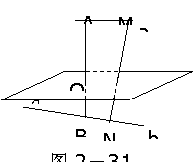如图2－31：设a、b是异面直线，A∈a，B∈b，AB⊥a，AB⊥b，过AB的中点O作平面α与a、b分别平行，M、N分别是a、b上任意两点，MN与α交于点P， 求证：P是MN的中点。 　 证明：连结AN，交平面α于点Q，连结PQ，OQ。 ∵　b//α，b平面ABN，平面ABN∩α＝OQ， ∴b// OQ，又O为AB有中点，∴Q为AN的中点。 ∵a//α，a 平面AMN，平面AMN∩α＝PQ， ∴a// PQ， ∴P是MN的中点。

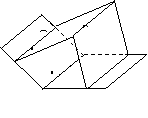
223. 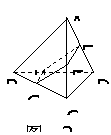如图2－29：四面体A－BCD被一平面所截，截面EFGH是一个矩形， (1)求证：CD//平面EFGH； (2)求异面直线AB、CD所成的角。 　证明：(1)∵截面EFGH是一个矩形， ∴EF//GH，又GH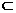平面BCD ∴EF//平面BCD，而EF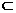平面ACD，面ACD∩面BCD＝CD ∴EF// CD，∴CD//平面EFGH 解：(2)则(1)知EF// CD，同理AB//FG， 由异面直线所成角的定义知∠EFG即为所求的角。 ∴AB、CD所成的角为90°

222. 求证：一条直线与两个相交平面都平行，则这条直线与这两个相交平面的交线平行。 已知：如图：a//α,a//β,α∩β＝b，求证：a//b

解析：　 本题可利用线面平行的性质定理来证明线线平行。

证明:　　 如图2－28，过a作平面γ、δ，使得γ∩α＝c，δ∩β＝d，那么有 　

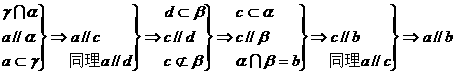
点评:　 本题证明过程，实际上就是不断交替使用线面平行的判定定理、性质定理及公理4的过程。这是证明线线平行的一种典型的思路。

221. 如图2－63，已知平面α⊥平面γ，平面β⊥平面γ。α∩γ＝a，β∩γ＝b且a∥b，求证α∥β。 证明：在平面γ内作直线c⊥a， 　　　　 ∵a∥b，∴c⊥b。 　　∵α⊥γ，∴c⊥α， 　　又∵β⊥γ，∴c⊥β， 　　∴α∥β