439. 直线a、b均在平面a 外，若a、b在平面a 上的射影是两条相交直线，则a和b的位置关系是(　)．

　A．异面直线　 　　　B．相交直线 　　　C．平行直线　 　　　D．相交或异面直线

解析：D

438. 若直线l与平面a 所成角为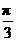，直线a在平面a 内，且与直线l异面，则直线l与直线a所成的角的取值范围是(　)．

　A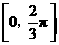．　　　　　　　　　　　　　 B．

　C．　　　　　　　　　　　　 　D．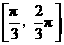

解析：C．因为直线l是平面的斜线，斜线与平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角，故a与l所成的角大于或等于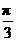；又因为异面直线所成的角不大于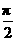，故选C．

437. 已知a、b是异面直线，那么经过b的所在平面中(　)．

　A．只有一个平面与a平行　 　　　　　　B．有无数个平面与a平行

　C．只有一个平面与a垂直 　　　　　　　D．有无数个平面与a垂直

解析：A．过b上任一点P作直线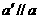，由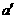和b确定的平面a 与a平行，这个平面是过b且平行于a的唯一一个平面．故排除B．当a与b不垂直时，假设存在平面b ，使bb ，且a⊥b ，则a⊥b，这与a、b不垂直矛盾，所以当a、b不垂直时，不存在经过b且与a垂直的平面，当a、b垂直时，过b且与a垂直的平面是唯一的，设a、b的公垂线为c，则由c和b所确定的平面与a垂直，且唯一．

436. 空间四边形ABCD的四条边相等，那么它的两条对角线AC和BD的关系是(　)．

　A．相交且垂直　 　　　　　　　　　　　B．相交但不垂直

　C．不相交也不垂直　 　　　　　　　　　D．不相交但垂直

解析：D．取BD中点O，则BD⊥AO，BD⊥CO，故BD⊥平面ACO，因此BD⊥AC．

435.　 圆柱形容器的内壁底半径为5cm，两个直径为5cm的玻璃小球都浸没于容器的水中，若取出这两个小球，则容器内的水面将下降　 　　cm.

解析：球的体积等于它在容器中排开水的体积.

解：　 设取出小球后，容器水平面将下降hcm，两小球体积为V_球＝2×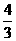π×5²×h,V₁＝　 V_球

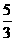即　 25πh＝π　 ∴h＝cm.

∴应填.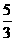

434.　 在球面上有四个点P、A、B、C.如果PA、PB、PC两两互相垂直，且PA＝PB＝PC＝a,那么这个球的表面积是　 　　　.

解析：由已知可得PA、PB、PC实际上就是球内接正方体中交于一点的三条棱，正方体的对角线长就是球的直径，连结过点C的一条对角线CD，则CD过球心O，对角线CD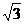＝a.

∴S_球表面积＝4π·(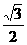a)²＝3πa².

433.　 长方体的一个顶点上的三条棱分别是3、4、5，且它的八个顶点都在同一球面上，这个球的表面积是(　　 )

A.20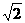π　　　　　 B.25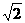π　　　　　 C.50π　　　　　 D.200π

解析： 正方体的对角线为l，球的半径为R，则l＝2R.

得：l²＝4R²＝3²+4²+5²＝50

从而　 S_球＝4πR²＝50π

∴应选C.

432.　 已知球面上A、B、C三点的截面和球心的距离都是球半径的一半，且AB＝BC＝CA＝2，则球表面积是(　　 )

A.π　　　　 B.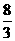π　　　　　 C.4π　　　　　 D.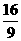π

解析： 如图，过ABC三点的截面圆的圆心是O′，球心是O，连结AO′、OO′，则OO′⊥　　　 AO′.ΔABC中，AB＝BC＝CA＝2，故ΔABC为正三角形.

∴AO′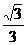＝×2＝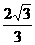

设球半径为R，则OA＝R，OO′＝

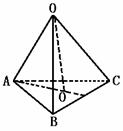
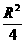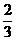
在RtΔOAO′中，OA²＝O′O²+O′A²，即R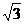²＝+()²

∴R＝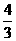

∴球面面积为4πR²＝π

∴应选A.

说明 　因为R＝OA＞O′A＞AB＝1，所以球面积S＝4πR²＞4π.从而选A.

431.　 球面上有3个点，其中任意两点的球面距离都等于大圆周长的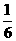，经过3个点的小圆的周长为4π，那么这个球的半径为(　　 )

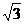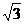A.4　　　　 B.2　　　　 C.2　　　　　 D.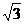

解析： 设球半径为R，小圆半径为r，则2πr＝4π,∴r＝2.如图，设三点A、B、C，O为球心，∠AOB＝∠BOC＝∠COA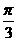＝，又∵OA＝OB

∴ΔAOB是等边三角形

同理，ΔBOC、ΔCOA都是等边三角形，得ΔABC为等边三角形.

边长等于球半径R，r为ΔABC的外接圆半径.

r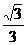＝AB＝R

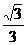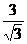R＝r＝2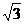

∴应选B.

450. 四面体对棱长分别相等，分别是a,b,c.求体积.

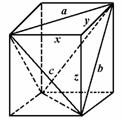
解析： 把四面体“嵌入”棱长为x,y,z的长方体(如图).其充分条件是

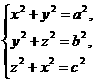
有实数解

如果关于x,y,z的方程组有实数解，则四面体体积

V＝xyz-4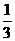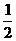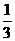··(xy)·z＝xyz

＝

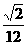
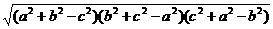
说明　 对棱相等的四面体各面是全等的锐角三角形，本题采用了体积分割法，转化法求体积.