418.　 已知四点，无三点共线，则可以确定(　　 )

A.1个平面　　　　　　　 B.4个平面

C.1个或4个平面　　　　 D.无法确定

解析： 因为无三点共线，所以任意三个点都可以确定平面α，若第四个点也在α内，四个点确定一个平面，当第四个点在α外，由公理3知可确定4个平面.故选C.

417.　 下列命题正确的是(　　 )

A.经过两条直线有且只有一个平面

B.经过一条直线和一个点有且只有一个平面

C.如果平面α与β有三个公共点，则两个平面一定是重合平面

D.两个平面α、β有一个公共点，那么它们有且只有一条通过这个点的公共直线

解析：根据公理2、公理3知选D.

416.　 空间可以确定一个平面的条件是(　　 )

A.两条直线　　　　　　　 B.一点和一直线

C.一个三角形　　　　　　 D.三个点

解析： 由推论2和推论3知两条相交直线或者两条平行直线才确定一个平面，两条直线还有位置关系异面.故排除A，由推论1知点必在线外才合适，排除B.由公理3知不共线三点可确定一个平面，D中三个点不一定不共线，排除D.公理3结合公理1，知选C.

415.过已知直线外一点与这条直线上的三点分别画三条直线，证明：这三条直线在同一平面内.

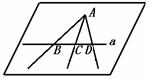
解答：已知：A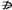a，如图，B、C、D∈a，证明：AB、AC、AD共面.

证明：∵A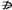a，∴A，a确定平面α，∵B、C、D∈a，a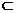α.

∴B、C、D∈α

又A∈α.

∴AB、AC、AD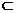α.

即AB、AC、AD共面.

414.一条直线过平面内一点与平面外一点，它和这个平面有几个公共点?为什么?

解析：只有一个，假设有两个公共点，由公理1知该直线上所有点都在这个平面内，这和直线过平面外一点矛盾.

413.　 证明推论3成立.(如图)

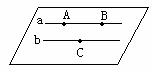
已知：a∥b，求证：经过a,b的平面有且只有一个.

证明：(存在性)∵a∥b，由平行线的定义知：a、b共面，所以经过a、b的平面有一个.

(唯一性)，在a上取两点A、B，在b上取一点C.

∵a∥b,∴A、B、C三点不共线，由公理3知过A、B、C三点的平面只有一个，从而过a,b两直线的平面也是惟一的.

412.　 证明两两相交而不共点的四条直线在同一平面内.

已知：如图，直线l₁，l₂，l₃，l₄两两相交，且不共点.

求证：直线l₁，l₂，l₃，l₄在同一平面内

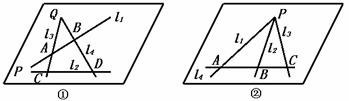
解析：证明几条直线共面的依据是公理3及推论和公理1.先证某两线确定平面α，然后证其它直线也在α内.

证明：图①中，l₁∩l₂＝P，

∴　 l₁,l₂确定平面α.

又　 l₁∩l₃＝A,l₂∩l₃＝C,　 ∴ C,A∈α.

故　 l₃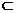α.

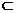同理　 l₄α.

∴　 l₁,l₂,l₃,l₄共面.

图②中，l₁,l₂,l₃,l₄的位置关系，同理可证l₁,l₂,l₃,l₄共面.

所以结论成立.

411.　 直线m、n分别和平行直线a、b、c都相交，交点为A、B、C、D、E、F，如图，求证：直线a、b、c、m、n共面.

解析： 证明若干条直线共面的方法有两类：一是先确定一个平面，证明其余的直线在这个平面里；二是分别确定几个平面，然后证明这些平面重合.

证明　 ∵a∥b,∴过a、b可以确定一个平面α.

∵A∈a,aα，∴A∈α,同理B∈a.

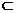又∵A∈m，B∈m,∴mα.同理可证nα.

∵b∥c,∴过b,c可以确定平面β，同理可证m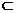β.

∵平面α、β都经过相交直线b、m,

∴平面α和平面β重合，即直线a、b、c、m、n共面.

2.在球心的同一侧有相距9cm的两个平行截面，它们的面积各为49πcm²和400πcm².求球的表面积.

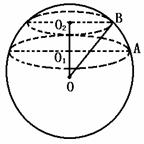
解：　 如图，设球的半径为R，

∵πO₂B²＝49π，　 ∴O₂B＝7

同理　 O₁A＝20

设OO₁＝xcm，则OO₂＝(x+9)cm.

在RtΔOO₁A中，可得R²＝x²+20²

在RtΔOO₂B中，可得R²＝7²+(x+9)²

∴x²+20²＝7²+(x+9)²

解方程得　 x＝15cm

R²＝x²+20²＝25²

∴S_球＝4π·OA²＝2500π(cm²)

430.求证：球的任意两个大圆互相平分.

证明：因为任意两个大圆都过球心O，所以它们必交于过球心的直径，这条直径也是两个大圆的公共直径，所以任意两个大圆互相平分.