
题目列表(包括答案和解析)
398. 平面α内有半径为R的⊙O,过直径AB的端点A作PA⊥α,PA=a,C是⊙O上一点,∠CAB=600,求三棱锥P-OBC的侧面积。
解析:三棱锥P-OBC的侧面由△POB、△POC、△PBC三个三角形组成
在求出边长元素后,求三角形面积时,应注意分析三角形的形状,简化计算
 ∵ PA⊥平面ABC
∵ PA⊥平面ABC
∴ PA⊥AO,AC为PC在平面ABC上的射影
∵ BC⊥AC
∴ BC⊥PC
△
POB中,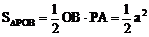
△
PBC中,BC=ABsin600=2a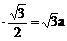
∴ AC=a
∴ PC=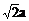
∴ 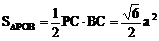
△
POC中,PO=PC=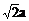 ,OC=a
,OC=a
∴ 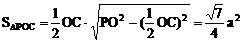
∴ S侧=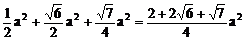
397. 斜三棱柱ABC-A1B1C1中,底面是边长为4cm的正三角形,侧棱AA1与底面两边AB、AC均成600的角,AA1=7
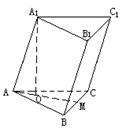 (1)求证:AA1⊥BC;(2)求斜三棱柱ABC-A1B1C1的全面积;(3)求斜三棱柱ABC-A1B1C1的体积;(4)求AA1到侧面BB1C1C的距离。
(1)求证:AA1⊥BC;(2)求斜三棱柱ABC-A1B1C1的全面积;(3)求斜三棱柱ABC-A1B1C1的体积;(4)求AA1到侧面BB1C1C的距离。
解析:设A1在平面ABC上的射影为0
∵ ∠A1AB=∠A1AC
∴ O在∠BAC的平行线AM上
∵ △ABC为正三角形
∴ AM⊥BC
又AM为A1A在平面ABC上的射影
∴ A1A⊥BC
(2)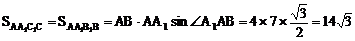
∵ B1B∥A1A
∴ B1B⊥BC,即侧面BB1C1C为矩形
∴ 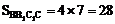
又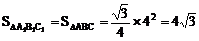
∴ S全=
(3)∵ cos∠A1AB=cos∠A1AO·cos∠OAB
∴ cos∠A1AO=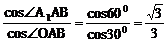
∴ sin∠A1AO=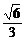
∴ A1O=A1Asin∠A1AO=
∴ 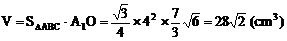
(4)把线A1A到侧面BB1C1C的距离转化为点A或A1到平面BB1C1C的距离
为了找到A1在侧面BB1C1C上的射影,首先要找到侧面BB1C1C的垂面
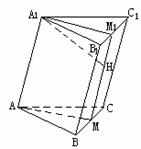 设平面AA1M交侧面BB1C1C于MM1
设平面AA1M交侧面BB1C1C于MM1
∵ BC⊥AM,BC⊥A1A
∴ BC⊥平面AA1M1M
∴ 平面AA1M1M⊥侧面BCC1B1
在平行四边形AA1M1M中
过A1作A1H⊥M1M,H为垂足
则A1H⊥侧面BB1C1C
∴ 线段A1H长度就是A1A到侧面BB1C1C的距离
∴ 
396. 正三棱柱ABC-A1B1C1的底面边长为a,在侧棱BB1上截取BD=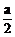 ,在侧棱CC1上截取CE=a,过A、D、E作棱柱的截面ADE
,在侧棱CC1上截取CE=a,过A、D、E作棱柱的截面ADE
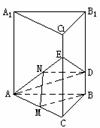 (1)求△ADE的面积;(2)求证:平面ADE⊥平面ACC1A1。
(1)求△ADE的面积;(2)求证:平面ADE⊥平面ACC1A1。
解析:分别在三个侧面内求出△ADE的边长
AE=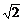 a,AD=
a,AD=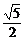 a,DE=
a,DE=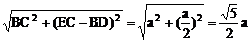
∴ 截面ADE为等腰三角形
S=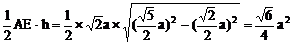
(2)∵ 底面ABC⊥侧面AA1C1C
∴ △ABC边AC上的高BM⊥侧面AA1C1C
下设法把BM平移到平面AED中去
取AE中点N,连MN、DN
∵ MN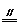
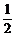 EC,BD
EC,BD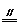
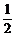 EC
EC
∴ MN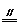 BD
BD
∴ DN∥BM
∴ DN⊥平面AA1C1C
∴ 平面ADE⊥平面AA1C1C
395. 已知直三棱柱ABC-A1B1C1中,∠ACB=900,∠BAC=300,BC=1,AA1=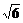 ,M为CC1中点,求证:AB1⊥A1M。
,M为CC1中点,求证:AB1⊥A1M。
解析: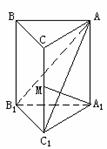 因结论是线线垂直,可考虑用三垂线定理或逆定理
因结论是线线垂直,可考虑用三垂线定理或逆定理
∵ ∠ACB=900
∴ ∠A1C1B1=900
即B1C1⊥C1A1
又由CC1⊥平面A1B1C1得:CC1⊥B1C1
∴ B1C1⊥平面AA1C1C
∴ AC1为AB1在平面AA1C1C的射影
由三垂线定理,下证AC1⊥A1M即可
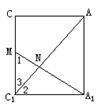 在矩形AA1C1C中,AC=A1C1=
在矩形AA1C1C中,AC=A1C1=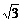 ,AA1=CC1=
,AA1=CC1=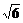
∵ 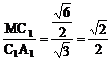 ,
,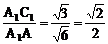
∴ 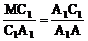
∴ Rt△A1C1M∽Rt△AA1C1
∴ ∠1=∠2
又∠2+∠3=900
∴ ∠1+∠3=900
∴ AC1⊥A1M
∴ AB1⊥A1M
评注:利用三垂线定理的关键是找到基本面后找平面的垂线
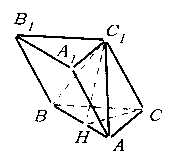
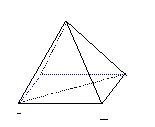
394. 如右图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角。
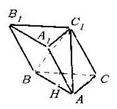 (1)求证:AC⊥面ABC1;
(1)求证:AC⊥面ABC1;
(2)求证:C1点在平面ABC上的射影H在直线AB上;
(3)求此三棱柱体积的最小值。
解析:(1)由棱柱性质,可知A1C1//AC
 ∵A1C1
∵A1C1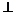 BC1,
BC1,
∴AC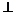 BC1,又∵AC
BC1,又∵AC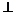 AB,∴AC
AB,∴AC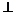 平面ABC1
平面ABC1
(2)由(1)知AC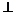 平面ABC1,又AC
平面ABC1,又AC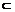 平面ABC,∴平面ABC
平面ABC,∴平面ABC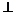 平面ABC1
平面ABC1
在平面ABC1内,过C1作C1H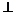 AB于H,则C1H
AB于H,则C1H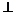 平面ABC,故点C1在平面ABC上
平面ABC,故点C1在平面ABC上
的射影H在直线AB上。
(3)连结HC,由(2)知C1H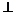 平面ABC,
平面ABC,
∴∠C1CH就是侧棱CC1与底面所成的角,
∴∠C1CH=60°,C1H=CH·tan60°=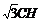
V棱柱=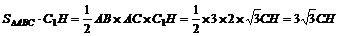
∵CA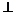 AB,∴CH
AB,∴CH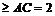 ,所以棱柱体积最小值3
,所以棱柱体积最小值3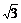
 。
。
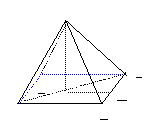
393. 正四棱锥的一个对角面与一个侧面的面积之比为
正四棱锥的一个对角面与一个侧面的面积之比为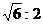 ,求侧面与底面所成的角的大小。
,求侧面与底面所成的角的大小。
解析:如图,正四棱锥P-ABCD的一个对角面△PAC。设棱锥的底面边长为a,高为h,斜高为h′,底面中心为O,连PO,则PO⊥底面ABCD,∴PO⊥AC,在△PAC中,AC=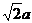 ,PO=h,
,PO=h,
 ∴
∴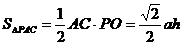
在△PBC中,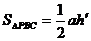 °
°
∴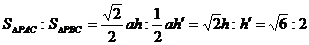
∴h:h′=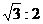 .
.
取BC中点E,连OE,PE,可证∠PEO即为侧面与底面所成两面角的平面角。
在Rt△POE中,sin∠PEO= ,
,
∴∠PEO=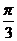 ,即侧面与底面所成的角为
,即侧面与底面所成的角为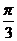 .
.
392. 如图,BCD是等腰直角三角形,斜边CD的长等于点P到BC的距离,D是P在平面BCD上的射影.(1)求PB与平面BCD所成角;(2)求BP与平面PCD所成的角
解析:(1)PD⊥平面BCD,∴BD是PB在平面BCD内的射影,∴∠PBD为PB与平面BCD所成角,BD⊥BC,由三垂线定理得BC⊥BD,∴BP=CD,设BC=a,则BD=a,BP=CD=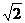 a∴在Rt△BPD中,
a∴在Rt△BPD中,
cos∠DBP=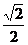 ∴∠DBP=45°, 即PB与平面BCD所成角为45°.
∴∠DBP=45°, 即PB与平面BCD所成角为45°.
(2)过B作BE⊥CD于E,连结PE,PD⊥平面BCD得PD⊥BE,∴BE⊥平面PCD,
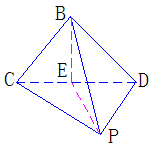
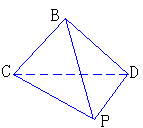 ∴∠BPE为BP与平面PCD所成的角,在Rt△BEP中,BE=
∴∠BPE为BP与平面PCD所成的角,在Rt△BEP中,BE=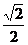 a, BP=
a, BP=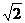 a,∴∠BPE=30°
即BP与平面PCD所成角为30°.
a,∴∠BPE=30°
即BP与平面PCD所成角为30°.
391. 如图,△ABC为锐角三角形,PA⊥平面ABC,A点在平面PBC上的射影为H,求:H不可能是△PBC的垂心.
解析: 连结CH,则CH是AC在平面PBC内的射影,若H为垂心,则CH⊥PB,由三垂线定理得AC⊥PB,又PA⊥平面ABC,∴PA⊥AC,∴AC⊥平面PAB,从而AC⊥AB与△ABC为锐角三
连结CH,则CH是AC在平面PBC内的射影,若H为垂心,则CH⊥PB,由三垂线定理得AC⊥PB,又PA⊥平面ABC,∴PA⊥AC,∴AC⊥平面PAB,从而AC⊥AB与△ABC为锐角三
角形矛盾,故H不可能是垂心.
410. 点P、Q、R分别在三棱锥A-BCD的三条侧棱上,且PQ∩BC=X,QR∩CD=Z,PR∩BD=Y.求证:X、Y、Z三点共线.
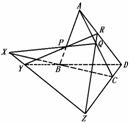
解析: 证明点共线的基本方法是利用公理2,证明这些点是两个平面的公共点.
证明 ∵P、Q、R三点不共线,∴P、Q、R三点可以确定一个平面α.
∵ X∈PQ,PQ α,∴X∈α,又X∈BC,BC
α,∴X∈α,又X∈BC,BC 面BCD,∴X∈平面BCD.
面BCD,∴X∈平面BCD.
∴ 点X是平面α和平面BCD的公共点.同理可证,点Y、Z都是这两个平面的公共点,即点X、Y、Z都在平面α和平面BCD的交线上.
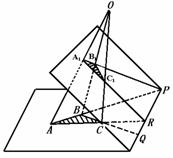
409. 若ΔABC所在的平面和ΔA1B1C1所在平面相交,并且直线AA1、BB1、CC1相交于一点O,求证:
(1)AB和A1B1、BC和B1C1、AC和A1C1分别在同一平面内;
(2)如果AB和A1B1、BC和B1C1、AC和A1C1分别相交,那么交点在同一直线上(如图).
(1)证明:∵AA1∩BB1=O,
∴AA1、BB1确定平面BAO,
∵A、A1、B、B1都在平面ABO内,
∴AB 平面ABO;A1B1
平面ABO;A1B1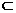 平面ABO.
平面ABO.
同理可证,BC和B1C1、AC和A1C1分别在同一平面内.
(2)分析:欲证两直线的交点在一条直线上,可根据公理2,证明这两条直线分别在两个相交平面内,那么,它们的交点就在这两个平面的交线上.
证明:如图,设AB∩A1B1=P;
AC∩A1C1=R;
∴ 面ABC∩面A1B1C1=PR.
∵ BC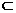 面ABC;B1C1
面ABC;B1C1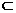 面A1B1C1,
面A1B1C1,
且 BC∩B1C1=Q ∴ Q∈PR,
即 P、R、Q在同一直线上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com