
题目列表(包括答案和解析)
388.
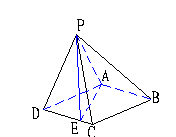
如图,在四棱锥P-ABCD中,侧面PCD是边长等于2cm的等边三角形,底面ABCD是面积为2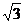 cm2的菱形,∠ADC是锐角.
cm2的菱形,∠ADC是锐角.
求证:PA⊥CD
证明:设∠ADC=θ,则:由SABCD=2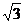 , CD=BC=AB=AD=2,易得θ=60°
, CD=BC=AB=AD=2,易得θ=60°
∴△ACD是等边三角形,取CD中点E连AE、PE,则AE⊥CD,PE⊥CD
AE⊥CD,PE⊥CD ∴CD⊥平面PAE ∴CD⊥PA
387. 如图,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
(1)
 求证:MN⊥CD;
求证:MN⊥CD;
(2) 若∠PDA=45°,求证:MN⊥平面PCD.
证明 (1)连AC∩BD=O,连NO,MO,则NO∥PA.
∵PA⊥平面ABCD,∴NO⊥平面ABCD.
∵MO⊥AB,∴MN⊥AB,而CD∥AB,∴MN⊥CD;
(2)∵∠PDA=45°,∴PA=AD,
由△PAM≌△CBM得PM=CM,
∵N为PC中点,∴MN⊥PC.
 又MN⊥CD,PC∩CD=C,∴MN⊥平面PCD.
又MN⊥CD,PC∩CD=C,∴MN⊥平面PCD.
386. P是边长为a的六边形ABCDEF所成平面外一点,PA⊥AB,PA⊥AF,PA=a,则点P到边CD的距离是
解析:2a.
PA⊥平面ABCDEF,A到CD的距离为 ,∴P到边CD的距离是2a
,∴P到边CD的距离是2a
385. △ABC在平面α内,∠C=90°,点P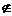 α,PA=PB=PC=7, AB=10, 则点P到平面α的距离等于
α,PA=PB=PC=7, AB=10, 则点P到平面α的距离等于
解析: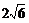 .
.
∵PA=PB=PC,∴P在平面α内的射影为△ABC的外心O,∵∠C=90°,∴O为AB的中点,∵AO=5,PA=7,∴PO=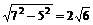
384. 直角三角形ABC的斜边AB在平面α内,直角顶点C在平面α外,C在平面α内的射影为C1,且C1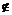 AB,则△C1AB为 ( )
AB,则△C1AB为 ( )
(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)以上都不对
解析:(C)
∵C1A2+C1B2<CA2+CB2 =AB, ∴∠AC1B为钝角,则△C1AB为钝角三角形.
383. 四面体ABCD的四个面中,是直角三角形的面至多有 ( )
(A)1个 (B)2个
(C)3个 (D)4个
解析:(D)
设底面为直角三角形,从底面的一个锐角顶点作平面的垂线,则这样的四面体的每个面都是直角三角形.
382. 如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,PA⊥平面ABCD,PA=a.
(1) 求证:PC⊥CD;
(2) 求点B到直线PC的距离.
解析:(1)要证PC与CD垂直,只要证明AC与CD垂直,可按实际情形画出底面图形进行证明.(2)从B向直线PC作垂直,可利用△PBC求高,但需求出三边,并判断其形状(事实上,这里的∠PBC=90°);另一种重要的思想是:因PC在平面PAC中,而所作BH为平面PAC的斜线,故关键在于找出B在平面PAC内的射影,因平面PAC处于“竖直状态”,则只要从B作“水平”的垂线,可见也只要从B向AC作垂线便可得其射影.
证明 (1)取AD的中点E,连AC,CE,
则ABCE是正方形,△CED为等腰直角三角形.
∴AC⊥CD,∵PA⊥平面ABCD,∴AC为PC在平面ABCD上的射影,∴PC⊥CD;
解 (2)连BE交AC于O,则BE⊥AC,
又BE⊥PA,AC∩PA=A,∴BE⊥平面PAC.
 过O作OH⊥PC于H,连BH,则BH⊥PC.
过O作OH⊥PC于H,连BH,则BH⊥PC.
∵PA=a,AC= ,∴PC=
,∴PC= ,则OH=
,则OH= ,
,
∵BO=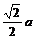 ,∴BH=
,∴BH=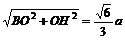
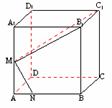
381. 如图,在正方体ABCD-A1B1C1D1中,M是棱A1A的中点,N在AB上,且AN∶NB=1∶3,求证:C1M⊥MN.
解析:在空间中作出两条直线垂直相对较在平面内作两条直线垂直难.此题C1M与MN是相交直线,一种方法可通过勾股定理来验证它是否垂直,另一方法为:因MN是平面A1ABB1内的一条直线,可考虑MC1在平面A1ABB1内的射影.
证明1 设正方体的棱长为a,则MN=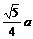 ,
,
C1M=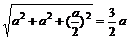 ,C1N=
,C1N=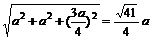 ,
,
∵MN2+MC12=NC12,∴C1M⊥MN.
证明2 连结B1M,∵C1B1⊥平面A1ABB1,
∴B1M为C1M在平面A1ABB1上的射影.
设棱长为a ,∵AN=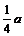 ,AM=
,AM=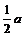 ,∴tan∠AMN=
,∴tan∠AMN=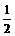 ,
,
又tan∠A1B1M=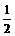 ,则∠AMN=∠A1B1M,∴B1M⊥MN,
,则∠AMN=∠A1B1M,∴B1M⊥MN,
由三垂线定理知,C1M⊥MN.
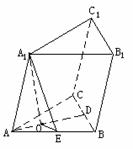
400. 斜三棱柱ABC-A1B1C1的底面△ABC中,AB=AC=10,BC=12,A1到A、B、C三点的距离都相等,且AA1=13,求斜三棱柱的侧面积。
解析:∵A1A=A1B=A1C
∴ 点A1在平面ABC上的射影为△ABC的外心,在∠BAC平分线AD上
 ∵ AB=AC
∵ AB=AC
∴ AD⊥BC
∵ AD为A1A在平面ABC上的射影
∴ BC⊥AA1
∴ BC⊥BB1
∴ BB1C1C为矩形,S=BB1×BC=156
取AB中点E,连A1E
∵ A1A=A1B
∴ A1E⊥AB
∴ 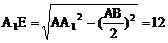
∴ 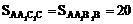
∴ S侧=396
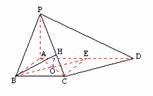
399. 四棱锥V-ABCD底面是边长为4的菱形,∠BAD=1200,VA⊥底面ABCD,VA=3,AC与BD交于O,(1)求点V到CD的距离;(2)求点V到BD的距离;(3)作OF⊥VC,垂足为F,证明OF是BD与VC的公垂线段;(4)求异面直线BD与VC间的距离。
解析:用三垂线定理作点到线的垂线
在平面ABCD内作AE⊥CD,E为垂足
∵ VA⊥平面ABCD
∴ AE为VE在平面ABCD上的射影
∴ VE⊥CD
∴ 线段VE长为点V到直线CD的距离
∵ ∠BAD=1200
∴ ∠ADC=600
∴ △ACD为正三角形
∴ E为CD中点,AE=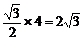
∴ VE=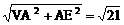
(2)∵ AO⊥BD
∴ 由三垂线定理VO⊥BD
∴ VO长度为V到直线BD距离
 VO=
VO=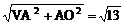
(3)只需证OF⊥BD
∵ BD⊥HC,BD⊥VA
∴ BD⊥平面VAC
∴ BD⊥OF
∴ OF为异面直线BD与VC的公垂线
(4)求出OF长度即可
在Rt△VAC中
OC=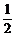 AC=2,VC=
AC=2,VC=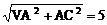
∴ OF=OC·sin∠ACF=OC·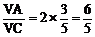
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com