598. 平面α∥平面β，A、B∈α，C∈β，AA′⊥β于A′，BB′⊥β于B′，若AC⊥AB，AC与β成60°的角，AC=8cm,B′C=6cm,求异面直线AC与BB′间的距离.

解析：∵BB′⊥α∴BB′⊥AB　 又∵AC⊥AB　 ∴AB为AC与BB′的公垂线

又∵AB=A′B′　 AB∥A′B′　 AC⊥A′B′

∴A′C′⊥A′B′

A′B′=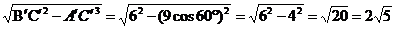

597. AB、CD为夹在两个平行平面α、β间的异面线段，M、N分别为AB、CD的中点，求证：MN∥α.

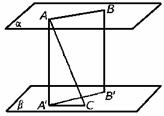
解析：过C作CE∥AB交β于E，取CE中点P则

AB∥CE　 AC∥BE　 MP∥AC　 BP∥α

(1)MP∥β；(2)PN∥ED?PN∥β.∴面MN∥面β∴MN∥面α，MN∥α

596.两条一异面直线所成的角的范围是？

直线与平面所成的角的范围是？

两个半平面所成二面角的范围是？

斜线与平面所成的角的范围是？

解析：，

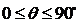，直线在平面内或直线与平面平行定为0

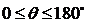，规定两个半平面重合时为0，两个半平面展成一个平面为180度。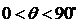

595. 直线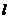与平面α所成角θ的范围是(　 )

　A、0°<θ<90°　　 B、0°θ90°　 C、0°<θ<180°　 D、0°θ180°

解析：B

594. 经过两条平行直线，有且只有一个平面

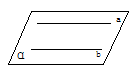证明：因为当两条直线在同一个平面内，且不相交时叫做平行线，所以两条平行直线a和b必在某个平面α内，就是说过两条平行直线有一个平面．如果过a和b还有一个平面β，那么在a上的任意一点A一定在β内这样过点A和直线b有两个平面α和β，这和推论1矛盾，所以过平行直线a和b的平面只有一个．

593. 经过两条相交直线，有且只有一个平面

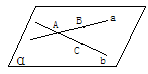　　 证明：如图：设直线a、b相交于点A，在a、b上分别取不同于点A的点B、C，得不在一直线上的三点A、B和C，过这三点有且只有一个平面α(公理3)，因此a、b各有两点在平面α内，所以a、b在平面α内，因此平面α是过相交直线a、b的平面．

如果过直线a和b还有另一个平面β，那么A、B、C三点也一定都在平面β内，这样过不在一条直线上的三点A、B、C就有两个平面α、β了，这和公理3矛盾，所以过直线a、b的平面只有一个．

592. 直线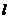上有两点到平面α的距离相等，这条直线和平面α的位置如何？

解析：(1)若直线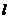上的两点到平面α的距离都等于0，这时直线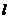在平面α内(如图)

(2)若直线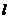上的两点在平面α的两侧,且到平面α的距离相等,这时直线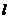与平面α相交(如图)．

(3)若直线l上的两点在平面α的同一侧，且到平面α的距离相等(如图)．

∵AA₁⊥α于点A₁，BB₁⊥α于点B₁．又 A、B均在l上，且在α的同侧．∴AA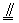₁ BB₁

∴AA₁BB₁为一平行四边形．∴AB∥A₁B₁ ∴这时直线l与平面α平行．

想一想：若直线l上各点到平面α的距离都相等，那么直线l和平面α的位置关系又怎样？

591. 两个惟一性定理．

(1)过一点有且只有一条直线和一已知平面垂直

(2)过一点有且只有一个平面和一已知直线垂直

过点A垂直于直线a的所有直线都在过点A，且垂直于直线a的平面内，试证之．

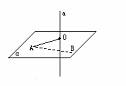已知：A∈α，a⊥α于点O，AB⊥a．求证：

证明：假AB不在平面α内，连结AO．

∵a⊥α∴a⊥AO．又a⊥AB，且AO∩AB=A．

∴a垂直于相交直AO、AB所确定的平面β．

说明：　关于直线和平面垂直的问题中，有两个基本作图：

(1)过一点有且只有一条直线和一个平面垂直．(2)过一点有且只有一个平面和一条直线垂直．

这两个基本作图可作为公理直接使用．

310.　 平面α内有一个半圆，直径为AB，过A作SA⊥平面α，在半圆上任取一点M，连SM、SB，且N、H分别是A在SM、SB上的射影.(1)求证：NH⊥SB.(2)这个图形中有多少个线面垂直关系?(3)这个图形中有多少个直角三角形?(4)这个图形中有多少对相互垂直的直线?

解析：此题主要考查直线与直线，直线与平面的垂直关系及论证，空间想象力.

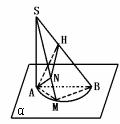
解　 (1)连AM，BM.∵AB为已知圆的直径，如图所示.

∴AM⊥BM，

∵SA⊥平面α，MBα，

∴SA⊥MB.

∵AM∩SA＝A，∴BM⊥平面SAM.

∵AN平面SAM，

∴BM⊥AN.

∵AN⊥SM于N，BM∩SM＝M，

∴AN⊥平面SMB.

∵AH⊥SB于H，且NH是AH在平面SMB的射影

∴NH⊥SB.

(2)由(1)知，SA⊥平面AMB，BM⊥平面SAM.AN⊥平面SMB.

∵SB⊥AH且SB⊥HN.

∴SB⊥平面ANH.

∴图中共有4个线面垂直关系

(3)∵SA⊥平面AMB，

∴ΔSAB、ΔSAM均为直角三角形.

∵BM⊥平面SAM，∴ΔBMA，ΔBMS均为直角三角形.

∵AN⊥平面SMB.∴ΔANS、ΔANM、ΔANH均为直角三角形.

∵SB⊥平面AHN.　 ∴ΔSHA、ΔBHA、ΔSHN均为直角三角形

综上所述，图中共有10个直角三角形.

(4)由SA⊥平面AMB知：SA⊥AM，SA⊥AB，SA⊥BM；

由BM⊥平面SAM知：BM⊥AM，BM⊥SM，BM⊥AN；

由AN⊥平面SMB知：AN⊥SM，AN⊥SB，AN⊥NH；

SB⊥平面AHN知：SB⊥AH，SB⊥HN；

综上所述，图中有11对互相垂直的直线.

309.　 在空间四边形ABCP中，PA⊥PC，PB⊥BC，AC⊥BC.PA、PB与平面ABC所成角分别为30°和45°。(1)直线PC与AB能否垂直?证明你的结论；(2)若点P到平面ABC的距离为h，求点P到直线AB的距离.

解析：主要考查直线与直线、直线与平面的位置关系的综合应用及线面角，点面间距离等概念应用，空间想象力及推理能力.

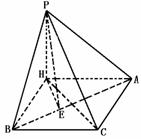
解 　(1)AB与PC不能垂直，证明如下：假设PC⊥AB，作PH⊥平面ABC于H，则HC是PC在平面ABC的射影，∴HC⊥AB，∵PA、PB在平面ABC的射影分别为HB、HA，PB⊥BC，PA⊥PC.

∴BH⊥BC，AH⊥AC

∵AC⊥BC，∴平行四边形ACBH为矩形.

∵HC⊥AB，∴ACBH为正方形.

∴HB＝HA

∵PH⊥平面ACBH.∴ΔPHB≌ΔPHA.

∴∠PBH＝∠PAH，且PB，PA与平面ABC所成角分别为∠PBH，∠PAH.由已知∠PBH＝45°，∠PAH＝30°，与∠PBH＝∠PAH矛盾.

∴PC不垂直于AB.

(2)由已知有PH＝h,∴∠PBH＝45°

∴BH＝PH＝h.∵∠PAH＝30°，∴HA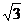＝h.

∴矩形ACBH中，AB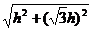＝＝＝2h.

作HE⊥AB于E，∴HE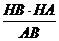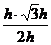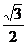＝＝＝h.

∵PH⊥平面ACBH，HE⊥AB，

由三垂线定理有PE⊥AB，∴PE是点P到AB的距离.

在RtΔPHE中，PE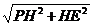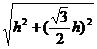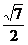＝＝＝h.

即点P到AB距离为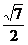h.

评析：此题属开放型命题，处理此类问题的方法是先假设结论成立，然后“执果索因”，作推理分析，导出矛盾的就否定结论(反证法)，导不出矛盾的，就说明与条件相容，可采用演绎法进行推理，此题(1)属于反证法.