
题目列表(包括答案和解析)
588. 在四面体ABCD中,已知点M,N,P分别在棱AD,BD,CD上,点S在平面ABC内,画出线段SD与过点M,N,P的截面的交点O。
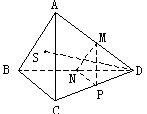 解析:图中,SD与平面MNP的交点O点画在△MNP内的任何位置好象都“象”,即直观上不能直接看出画在何处才是准确的。采用上一题的思想方法,找出经过直线SD的平面,如平面ASD(平面CSD…),作出它与平面MNP的交线。
解析:图中,SD与平面MNP的交点O点画在△MNP内的任何位置好象都“象”,即直观上不能直接看出画在何处才是准确的。采用上一题的思想方法,找出经过直线SD的平面,如平面ASD(平面CSD…),作出它与平面MNP的交线。
解:连接AS交BC于E,连ED交NP于F,连MF。
∵M∈AD,AD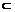 平面AED,
平面AED,
∴M∈平面AED
∵F∈ED,ED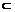 平面AED,
平面AED,
∴F∈平面AED
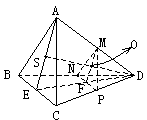 又M∈平面MNP,F∈平面MNP,
又M∈平面MNP,F∈平面MNP,
∴平面AED∩平面MNP=MF
∵O∈SD,SD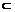 平面AED,
平面AED,
∴O∈平面AED,又O∈平面MNP
则O∈MF
即O为MF与SD的交点。
587. 四面体ABCD中,AB=CD,AC=BD,AD=BC,则∠BAC+∠CAD+∠DAB= 。
解析:180°
四个三角形均是全等的三角形,故所求三个角即其中任一三角形的三个内角
586. 正方体的12条面对角线所在的直线中,互相异面的直线共有 对。
解析:30
面对角线中,与AC相交的有5条,平行的有1条,(自身为1条)故与AC异面的直线有12-5-1-1=5(条)。
则共有12×5×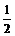 =30(对
=30(对
585. 空间两个角α和β,若α和β的两边对应平行,当α=50°时,β= 。
解析:50°或130°
β与α相等或互补
584. 下面的三个命题:①四边相等的四边形是菱形;②两组对边分别相等的四边形是平行四边形;③若四边形有一组对角都是直角,则这个四边形是圆的内接四边形。
其中正确命题的个数是:( )
A、1个 B、2个 C、3个 D、0个
 解析:D
解析:D
均不能保证它们是平面图形,故均不正确,选D
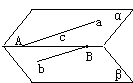
583. 如图,α∩β=C,a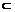 α,a∩c=A,b
α,a∩c=A,b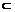 β,b∩c=B,A、B为不同点。则a与b的位置关系为( )
β,b∩c=B,A、B为不同点。则a与b的位置关系为( )
 A、平行
A、平行
B、异面
C、平行、异面均可能
D、平行、相交、异面均可能
解析:B
符合两条异面直线的判定,选B
582. 如图,在正方体ABCD--A1B1C1D1中,E、F分别是B1D1,A1B的中点,求证:EF∥AD1。
解析:要证两条直线平行一是证这两条直线在同一平面内,再用平面几何知识证明它们平行;二是用平行公理即平行直线的传递性,找到与它们都平行的“公共”直线。
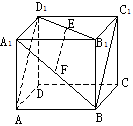 这里E为D1B1的中点,易想到用构造三角形的中位线的方法直接证明平行。因此,连AB1是非常重要的步骤。
这里E为D1B1的中点,易想到用构造三角形的中位线的方法直接证明平行。因此,连AB1是非常重要的步骤。
证明:连AB1,则AB1过A1B的中点F。
又E为D1B1的中点,
∴EF为△AD1B1的中位线,
则EF∥AD1
581.
已知空间四边形ABCD中,E、H分别是AB、AD的中点。(1)如图(甲)中,F、G分别是BC、CD的中点,求证:四边形EFGH是平行四边形;(2)如图(乙)中,若F是BC上的点,G是DC上的点,且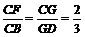 ,求证:四边形EFGH是梯形,并且直线EF、GH、AC共点。
,求证:四边形EFGH是梯形,并且直线EF、GH、AC共点。
证明:(1)如图(甲),连结BD。
∵EH是的△ABD中位线,
∴EH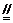
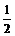 BD,同理FG
BD,同理FG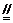
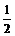 BD
BD
根据公理4,EH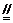 FG
FG
∴四边形EFGH是平行四边形。
(2)如图(乙)由(1)知EH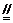
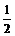 BD,又在△ABD中,
BD,又在△ABD中,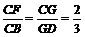
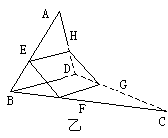 ∴FG∥BD,FG=
∴FG∥BD,FG=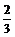 BD
BD
由公理4,∴EH∥FG,又FG>EH。
∴四边形EFGH是梯形。
则直线EF、GH相交,设EF∩GH=P
则P∈EF,又EF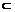 平面ABC
平面ABC
∴P∈平面ABC,同理P∈平面ADC。
又平面ABC∩平面ADC=AC
由公理2,得P∈AC,
即EF、GH、AC三条直线共点。
点评:证明四边形是平行四边形或者梯形,首先必须证明它是平面图形,本题中的EH∥FG是关键
600. 要修建一座底面是正方形且四壁与底面垂直的水池,在四壁与底面面积之和一定的前提下,为使水池容积最大,求水池底面边长与高的比值.
解析:为了建立体积V的函数,我们选底面边长和高为自变量.
设水池底面边长为a,水池的高为h,水池容积为v,依题意,有a2+4ah=k(k为定值).
∴v=a2h=a2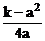 =
=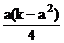 (v>0),
(v>0),
∴v2=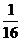 a2(k-a2)2=
a2(k-a2)2=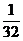 ·2a2(k-a2)(k-a2)
·2a2(k-a2)(k-a2)
≤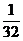 (
(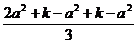 )3=
)3=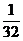 ·
·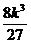 =
=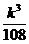 (当且仅当2a2=k-a2时,即k=3a2时等号成立),
(当且仅当2a2=k-a2时,即k=3a2时等号成立),
故 a2+4ah=3a2,
即a∶h=2∶1时,水池容积最大为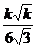 .
.
599. 某人买了一罐容积为V升、高为a米的直三棱柱型罐装进口液体车油,由于不小心摔落地上,结果有两处破损并发生渗漏,它们的位置分别在两条棱上且距底面高度分别为b、c的地方(单位:米).为了减少罐内液油的损失,该人采用罐口朝上,倾斜罐口的方式拿回家.试问罐内液油最理想的估计能剩多少?
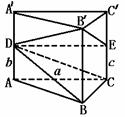
解析:如图所示,建立模型,设直三棱柱为ABC-A′B′C′,破损处为D、E.并且AD=b,EC=c,BB′=a.则罐内所剩液油的最大值即为几何体ABC-DB′E的体积.
连结BD、CD
∵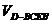 =
=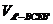 ,
,
而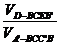 =
=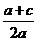 ,
,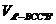 =
=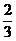 V,
V,
∴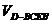 =
=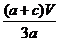 .
.
又∵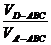 =
= ,∴VD-ABC=
,∴VD-ABC= ·
·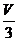 =
=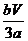 .
.
故 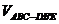 =
=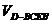 +VD-ABC=
+VD-ABC=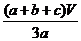 ,即最理想的估计是剩下
,即最理想的估计是剩下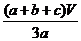 升.
升.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com