
题目列表(包括答案和解析)
578. 正方体ABCDA1B1C1D1中,若E、M、N分别是棱AB、BC及B1D1的中点,求异面直线DN与MC1所成的角。
解析:连NG、EM、EN、DE
∵ EM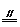
 AC,NC1
AC,NC1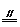
 AC
AC
∴ NC1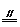 EM
EM
∴ NE∥MC1
∴ ∠DNE为异面直线DN与MC1所成的角
设AB=a,则DE=EN=GM= ,DN=
,DN=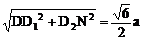
△
DNE中,cos∠DNE=
∴ 异面直线DN与MC1所成的角为arccos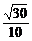 .
.
577.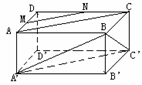 长方体ABCD-A’B’C’D’中,AB=2,BC=BB’=1,M、N分别是AD和BC中点,求异面直线MN和BC’所成角的大小
长方体ABCD-A’B’C’D’中,AB=2,BC=BB’=1,M、N分别是AD和BC中点,求异面直线MN和BC’所成角的大小
解析:∵MN∥AC,AC∥A’C’,∴MN∥A’C’
∴ ∠BC’A’就是MN与BC’所成的角
△
BA’C中,BC’= ,BA’=A’C’=
,BA’=A’C’=
∴ cos∠BC’A’=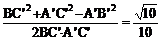
576.
M、N分别是空间四边形ABCD中AB、CD中点,求证:MN< (AD+BC)。
(AD+BC)。
证明:取AC中点P,则MP= BC,NP=
BC,NP= AD
AD
∴ MN<MP+NP= (BC+AD)
(BC+AD)
575. 长方体ABCD-A1B1C1D1中,AB=a,BC=b,AA1=c,求异面直线BD1和B1C所成角的余弦值。
解析:显然,通过平移在长方体的表面及内部不可能构造出一个BD1和B1C所成的角,但同时又为了使构造出的角便于计算,故可考虑补上一个与已知长方体相同的长方体DCEF-D1C1E1F1。具体作法是:延长A1D1,使A1D1=D1F1,延长B1C1至E1,使B1C1=C1E1,连E1F1,分别过E1、F1,作E1E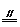 C1C,F1F
C1C,F1F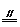 D1D,连EF,则长方体C1D1F1E-CDFE为所作长方体。
D1D,连EF,则长方体C1D1F1E-CDFE为所作长方体。
∵ BC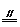 D1F1
D1F1
∴ BD1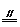 CF1
CF1
∴ ∠B1CF1就是异面直线BD1与B1C所成的角。
∵ BD2=a2+b2
∴ Rt△BDD1中,BD12=BD2+DD12=a2+b2+c2
∴ CF12=BD12=a2+b2+c2
∵ B1C2=b2+c2,B1F12=a2+4b2
∴ △B1CF1中
cos∠B1CF1=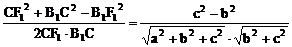
(1) 当c>b时, cos∠B1CF1>0
∴ ∠B1CF1为锐角,∠B1CF1就是异面直线BD1和B1C所成的角
(2) 当c<b时,cos∠B1CF1<0
∴ ∠B1CF1是钝角
∴ π-∠B1CF1就是异面直线BD1和B1C所成的角
(3) 当c=b时,∠B1CF1=900
∴ BD1⊥B1C
 法二:作异面直线所成角的过程,其实就是平移异面直线的过程。借助于三角形中位线的平行性,也可以达到平移的目的。
法二:作异面直线所成角的过程,其实就是平移异面直线的过程。借助于三角形中位线的平行性,也可以达到平移的目的。
如图,分别取BC、BB1、B1D1的中点P、M、Q,连PM、MQ、PQ
则 MP∥B1C,MQ∥BD1
∴ ∠PMQ(或其补角)就是异面直线BD1与B1C所成的角
△
PMQ中,MP= B1C=
B1C=
△
MQ BD1=
BD1=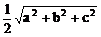 ,PQ=
,PQ=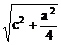
利用余弦定理可以得到与解法一同样的结果
574. 空间四边形DABC中,P、Q为边CD上两个不同的点,M、N为AB上两个不同的点,连PM、QN,如图,问图中共有多少对异面直线?
 解析:为使计算异面直线条数的过程中不出现重、漏的现象,可采用逐步添加的方法。首先考虑空间四边形DABC的四条边DA、AB、BC、CD连同对角线AC、BD,这六条线段可形成三对异面直线DA与BC,AB与CD,AC与BD。
解析:为使计算异面直线条数的过程中不出现重、漏的现象,可采用逐步添加的方法。首先考虑空间四边形DABC的四条边DA、AB、BC、CD连同对角线AC、BD,这六条线段可形成三对异面直线DA与BC,AB与CD,AC与BD。
其次添加线段PM,则除去与PM相交的CD、AB,又可新形成4对异面直线,即PM与DA、BC、AC、BD。
因QN与PM位置等同,当添上QN时,也同样新增4对异面直线。
最后注意到,PM与QN也是异面直线。
∴ 图中共有3+4+4+1=12(对)异面直线
573. 四棱锥V-ABCD底面是边长为4的菱形,∠BAD=1200,VA⊥底面ABCD,VA=3,AC与BD交于O,(1)求点V到CD的距离;(2)求点V到BD的距离;(3)作OF⊥VC,垂足为F,证明OF是BD与VC的公垂线段;(4)求异面直线BD与VC间的距离。
解析:用三垂线定理作点到线的垂线
在平面ABCD内作AE⊥CD,E为垂足
∵ VA⊥平面ABCD
∴ AE为VE在平面ABCD上的射影
∴ VE⊥CD
∴ 线段VE长为点V到直线CD的距离
∵ ∠BAD=1200
∴ ∠ADC=600
∴ △ACD为正三角形
∴ E为CD中点,AE=
∴ VE=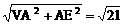
(2)∵ AO⊥BD
∴ 由三垂线定理VO⊥BD
∴ VO长度为V到直线BD距离
 VO=
VO=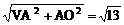
(3)只需证OF⊥BD
∵ BD⊥HC,BD⊥VA
∴ BD⊥平面VAC
∴ BD⊥OF
∴ OF为异面直线BD与VC的公垂线
(4)求出OF长度即可
在Rt△VAC中
OC= AC=2,VC=
AC=2,VC=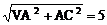
∴ OF=OC·sin∠ACF=OC·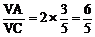
572. 斜三棱柱ABC-A1B1C1的底面△ABC中,AB=AC=10,BC=12,A1到A、B、C三点的距离都相等,且AA1=13,求斜三棱柱的侧面积。
解析:∵A1A=A1B=A1C
∴ 点A1在平面ABC上的射影为△ABC的外心,在∠BAC平分线AD上
 ∵ AB=AC
∵ AB=AC
∴ AD⊥BC
∵ AD为A1A在平面ABC上的射影
∴ BC⊥AA1
∴ BC⊥BB1
∴ BB1C1C为矩形,S=BB1×BC=156
取AB中点E,连A1E
∵ A1A=A1B
∴ A1E⊥AB
∴ 
∴ 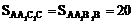
∴ S侧=396
571. 正三棱锥的侧棱等于10cm,侧面积等于144cm2,求棱锥的底面边长和斜高。
解析:设底面边长为a,斜高为h’
则 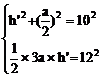
∴ 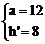 或
或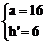
590. 空间四边形ABCD中,P、Q、R分别AB、AD、CD 的中点,平面PQR交BC于S , 求证:四边形PQRS为平行四边形。
证明:∵PQ为AB、AD中点 ∴PQ‖BD
又PQ 平面BCD ,BD
平面BCD ,BD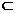 平面BCD
∴ PQ‖平面BCD
平面BCD
∴ PQ‖平面BCD
又平面PQR∩平面BCD=RS , PQ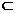 平面RQR ∴
PQ‖RS
平面RQR ∴
PQ‖RS


 ∵R为DC中点,∴ S为BC中点,∴PQ RS ∴ PQRS 为平行四边形
∵R为DC中点,∴ S为BC中点,∴PQ RS ∴ PQRS 为平行四边形
评述:灵活运用线面平行的判定定理和性质定理,“线线平行  线面平行”是证平行关系的常用方法。
线面平行”是证平行关系的常用方法。
变式题:如图,在四面体ABCD中,截面EFGH是平行四边形.求证:AB∥平面EFG.
证明 ∵面EFGH是截面.∴点E,F,G,H分别在BC,BD,DA,AC上.∴EH  面ABC,GF
面ABC,GF  面ABD,由已知,EH∥GF.∴EH∥面ABD.又 ∵EH
面ABD,由已知,EH∥GF.∴EH∥面ABD.又 ∵EH  面BAC,面ABC∩面ABD=AB∴EH∥AB.
面BAC,面ABC∩面ABD=AB∴EH∥AB.
∴AB∥面EFG.
589. 已知直线a∥b,c∩a=A,c∩b=B。求证:a、b、c在同一平面内。
 证明:∵a∥b
证明:∵a∥b
∴经过a、b可确定一个平面α
∵c∩a=A,∴A∈a,而a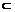 α
α
∴A∈α,同理B∈α
则AB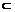 α,即c
α,即c 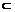 α
α
∴a、b、c在同一平面α内
点评:利用a∥b,可确定平面α,易证c 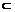 α。若利用c∩a=A,也可确定平面α,但证b
α。若利用c∩a=A,也可确定平面α,但证b α就较困难。因此,选择恰当的点或线确定平面是非常重要的。
α就较困难。因此,选择恰当的点或线确定平面是非常重要的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com