568. 正四棱柱ABCD-A₁B₁C₁D₁中，A₁B与对角面A₁B₁CD所成角为30⁰，求证：此四棱柱为正方体。

解析：∵ A₁B₁⊥平面B₁C

∴ 平面A₁B₁CD⊥平面BC₁，交线为B₁C

在平面B₁C内作BO⊥B₁C，O为垂足，连A₁O

则BO⊥平面A₁B₁CD

∴ ∠BA₁O为BA₁与平面A₁B₁CD所成的角

∴ ∠BA₁O=30⁰

设正四棱柱底面边长为a，高为h

则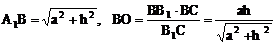

∵　sin∠BA₁O=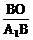

∴

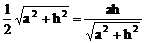
∴ a²+h²=2ah

∴ a=h

∴ 正四棱柱ABCD-A₁B₁C₁D₁为正方体

567. 一个正棱锥的一个侧面与底面所成角是θ，底面积Q，则它的侧面积是________。

解析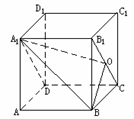： Qsecθ 　正棱锥的底面是侧面在底面上的射影，利用面积射影定理

566. 正六棱柱的高为5cm，最长对角线为13cm，它的侧面积是__________。

解析： 180cm² 　设正六棱柱底面边长为a，高为h，则h²+(2a)²=13²，h=5，∴a=6，∴侧面积=6ah=180

565. 正n棱柱每相邻两个侧面所成二面角度数为__________。

解析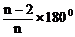：　 底面正多边形的每一个内角为某两个邻面所成二面角的平面角，正n边形内角度数为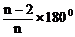

564. 正四棱柱的一个侧面面积为S，则它的对角面面积是__________。

解析：　 设正棱柱底面边长为a，高为h，则ah=S，对角面面积为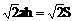

563. 在四棱锥的四个侧面中，直角三角形最多可有

A、1个　　　　　 B、2个　　　　　 C、3个　　　　　 D、4个

解析：D。 如图，ABCD为矩形，PA⊥平面ABCD，则P-ABCD的四个侧面均为直角三角形

562. 斜四棱柱侧面最多可有几个面是矩形

A、　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 0个　　　　　 B、1个　　　　　 C、2个　　　　　 D、3个

解析：C。 只能相对的侧面均为矩形

561. 四面体的四个顶点到平面M的距离之比为1∶1∶1∶3，则平面M的个数应有多少个?

解　 这样的平面应分4种情况讨论：

(1)4个顶点都在平面M的同侧，则有C₄¹·1＝4个(平面)；

(2)距离比为3的顶点与其他3个顶点不同侧，则有C₄¹·1＝4个(平面)；

(3)距离比为3的顶点与其他3个顶点中的1个同侧，则有C₃¹·C₄¹·1＝12个(平面)

(4)距离比为3的顶点与其他3个顶点中的2个同侧，则有C₃²·C₄¹·1＝12个(平面)；

∴　 一共应有4+4+12+12＝32个(平面)

580. 求证：空间四边形的两条对角线是异面直线。

证明：如图，假设空间四边形ABCD的对角线AC与BD不是异面直线。

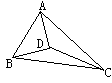则AC、BD共面于α，则A、B、C、D均在平面α内，这与已知“ABCD是空间四边形(四个顶点不在同一平面内)”相矛盾。

故假设错误，因此AC、BD是异面直线。

点评：反证法是间接证法的一种，在立体几何的证中经

常用到。

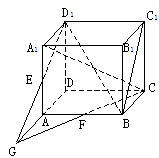
579. 如图，在正方体ABCD--A₁B₁C₁D­₁中，E、F分别是AA₁、AB的中点，试判断下列各对线段所在直线的位置关系：

　　 (1)AB与CC₁；(2)A₁B₁与DC；

(3)A₁C与D₁B；(4)DC与BD₁；

(5)D₁E与CF

解析：(1)∵C∈平面ABCD，AB平面ABCD

　　　　 又CAB，C₁平面ABCD

　　　　 ∴AB与CC₁异面

(2)∵A₁B₁∥AB，AB∥DC，∴A₁B₁∥DC

(3)∵A₁D₁∥B₁C₁，B₁C₁∥BC，∴A₁D₁∥BC

　　 则A₁、B、C、D₁在同一平面内

　　 ∴A₁C与D₁B相交

(4)∵B∈平面ABCD，DC平面ABCD

　　 又BDC，D₁平面ABCD

　　 ∴DC与BD₁异面

(5)如图，CF与DA的延长线交于G，连结D₁G，

　　 ∵AF∥DC，F为AB中点，

　　 ∴A为DG的中点，又AE∥DD₁，

　　 ∴GD₁过AA₁的中点E，

　　 ∴直线D₁E与DF相交