
题目列表(包括答案和解析)
548. α和β是两个不重合的平面,在下列条件中可以判定平面α∥β的是( )
A.α、β都垂直于平面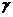
B.α内不共线的三点到β的距离相等
C.l、m是α内的直线,且l∥β,m∥β
D.l、m是两条异面直线,且l∥α,l∥β,m∥α,m∥β
解析:显然B、C不能推出α∥β,有α、β相交的情况存在,对于A、D,学了“面面垂直”后,就可以说明A不能推出α∥β,α、β有相交的可能,从而选D.
事实上,l∥α,m∥α,在α内任取一点A,过A作l′∥l,m′∥m,因为l,m异面,所以l′,m′相交,则可推出l′∥β,m′∥β.由面面平行的判定定理可推出α∥β.
547. 设a、b是两条异面直线,那么下列四个命题中的假命题是( )
A.经过直线a有且只有一个平面平行于直线b
B.经过直线a有且只有一个平面垂直于直线b
C.存在分别经过直线a和b的两个互相平行的平面
D.存在分别经过直线a和b的两个互相垂直的平面
解析:A、C、D均为真命题,B为假命题;∵若过a的平面α⊥b,则b垂直α内的直线a,从而a⊥b,那么限制a,b必须垂直,而条件中没有指明a、b是否垂直.
546. 设直线a在平面α内,则“平面α∥平面β”是“直线a∥平面β”的( )条件
A.充分但不必要 B.必要但不充分
C.充分且必要 D.不充分也不必要
解析:若α∥β,∵a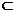 α,∴a与β无公共点,∴a∥β.
α,∴a与β无公共点,∴a∥β.
若a∥β,a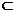 α,则α,β的关系不能确定,所以应选A.
α,则α,β的关系不能确定,所以应选A.
545.如图,直线AC、DF被三个平行平面α、β、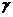 所截.
所截.
求证: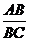 =
=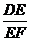
证:(i)当AC,DF共面S时,
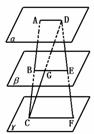
连AD,BE,CF
则AD∥BE∥CF
从而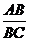 =
=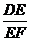
(ii)当AC、DE异面时,连CD设CD∩β=G
连AD、BG、GE、CF,如图
∵α∥β,平面ACD∩β=BG,平面ACD∩α=AD.
∴BG∥AD
∴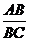 =
=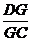
同理可证:EG∥CF,∴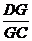 =
=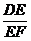
∴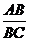 =
=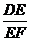
综合(i)(ii)知: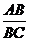 =
=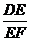 .
.
544.a和b是两条异面直线,求证:过a且平行b的平面必平行于过b且平行于a的平面.
已知:a,b是异面直线,a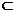 α,b
α,b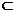 β,a∥β,b∥α.
β,a∥β,b∥α.
求证:α∥β.
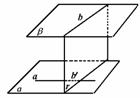
证:过b作平面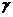 与平面α交于b′
与平面α交于b′

543.一条直线和两个平行平面相交,求证:它和两个平面所成的角相等.
已知:α∥β,直线a分别与α和β相交于点A和A′.
求证:a与α所成的角与a与β所成的角相等.
解析:(1)当a⊥α时,∵α∥β,∴α⊥β.
即a与α所成的角与a与β所成的角都是直角.
(2)当a是α的斜线时,如图,设P是a上不同于A、A′的任意一点,过点P引a′⊥α, a′∩α=B,a′∩β=B′.
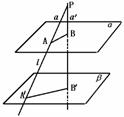
连结AB和A′B′.
∵a∥β,a′⊥α.
∴α′⊥β
由此可知,∠PAB是a和α所成的角,∠P′A′B是a和β所成的角,而AB∥A′B′.
∴∠PAB=∠PA′B′
即 a和α所成的角等于a和β所成的角.
542.经过平面外一点只有一个平面和已知平面平行.
已知:A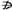 α,A∈β,β∥α
α,A∈β,β∥α
求证:β是唯一的.
证:设l过A点,且l⊥α,这样的直线是唯一的.
又β∥α,则β⊥l,过点A与α平面的平面一定和l垂直.
∵过点A和直线l垂直的平面是唯一的.
∴过点A和α平行的平面是唯一的.
541. 如图,已知直线a∥平面α;求证:过a有且只有一个平面平行于α.
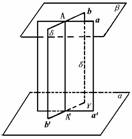
证明 (1)存在性:设过a的平面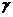 与α交于a′,∵a∥α,∴a∥a′.在α上,设直线b′∩a′=A′,在a上取点A,A与b′确定平面δ,在δ上过A作b∥b′.则a、b是相交直线(若重合,则显然b′∥a′,矛盾).∴a,b确定平面β,则β∥α.
与α交于a′,∵a∥α,∴a∥a′.在α上,设直线b′∩a′=A′,在a上取点A,A与b′确定平面δ,在δ上过A作b∥b′.则a、b是相交直线(若重合,则显然b′∥a′,矛盾).∴a,b确定平面β,则β∥α.
(2)唯一性:设过a还有一个平面π∥α,∵π与δ有公共点A,∴π与δ相交于过A的直线b″,又π∥a,δ∩b′,∴b″∥b′,∴b″∥b,而b″与b都过点A,故重合,故π与β重合.
560. 在ΔABC中,M、N分别是AB、AC上的点, =
=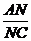 =
=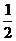 .沿MN把ΔAMN到ΔA′MN的位置,二面角A′-MN-B为60°,求证:平面A′MN⊥平面A′BC.
.沿MN把ΔAMN到ΔA′MN的位置,二面角A′-MN-B为60°,求证:平面A′MN⊥平面A′BC.
解析:作AD⊥BC于D,设AD∩MN=P,∠A′PD=60°,可证A′P⊥平面A′BC.
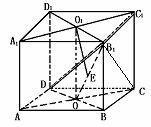
559. 正方体ABCD-A1B1C1D1的棱长为a,求A1C1和平面AB1C间的距离.
解法1 如图所示,A1C1∥平面AB1C,又平面BB1DD1⊥平面AB1C.
故若过O1作O1E⊥OB1于E,则OE1⊥平面AB1C,O1E为所求的距离
由O1E·OB1=O1B1·OO1,
可得:O1E=
解法2:转化为求C1到平面AB1C的距离,也就是求三棱锥C1-AB1C的高h.
由 V =V
=V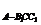 ,可得h=
,可得h= a.
a.
解法3 因平面AB1C∥平面C1DA1,它们间的距离即为所求,连BD1,分别交B1O、DO1与F、G(图中未画出)。易证BD1垂直于上述两个平面,故FG长即为所求,易求得
FG= .
.
点评 (1)求线面距离的先决条件是线面平行,而求线面距离的常用方法是把它们转化为求点面之间的距离,有时也可转化为求面面距离,从本题的解法也可悟出求异面直线之间的距离的思路.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com