
题目列表(包括答案和解析)
538. 如图,已知线段PQ、PD、QF分别和平行平面α、β交于A、B、C、D、E、F,若AP=BQ,求证:SΔACF=SΔBDE.
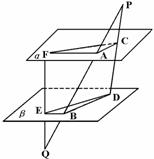
解析: 由已知得AC∥BD,EB∥AF,∠CAF=∠EBD,又AC∶BD=PA∶PB=QB∶QA=EB∶AF,∴AC·AF·sin∠CAF=BE·BD·sin∠DBE.∴SΔACF=SΔBDE.
537. 已知A,B∈平面α,C,D∈平面β,α∥β,AB=13,BD=15,AC、BD在平面α上的射影长之和是14,求AC、BD在平面α上的射影长,以及平面α、β的距离.
解 如图,设α、β的距离是h,则AC在α内的射影长是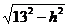 ,BD在α内的射影长是
,BD在α内的射影长是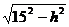 .
.
根据题意,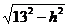 +
+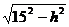 =14.
=14.
解这个方程,h=12.
∴ 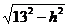 =5,
=5, 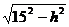 =9.
=9.
故AC、BD在平面α上的射影长分别是5和9,平面α、β的距离是12.
点评 平行平面间距离通常转化为点面距离或线面距离最终转化为点面距离.
536. 已知直线a、b、c,平面α∩平面β=a,b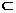 α,c
α,c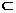 β,且b与c无公共点,则b与c不平行的充要条件是( )
β,且b与c无公共点,则b与c不平行的充要条件是( )
A.b、c都与α相交 B.b、c中只有一条与α相交
C.b、c中至多一条与α相交 D.b、c中至少有一条与α相交
解析:本题考查直线与直线的位置关系,直线与平面的位置关系,充要条件,以及空间想象能力和等价转化能力.
解法一:若直线b与c不平行,又由b与c无公共点,则b与c必定异面,根据异面直线的定义和线面位置关系可知或者b与c都与a相交,或者b、c中有一条与a相交,另一条与a平行,即b、c中至少有一条与α相交,即D成立;反之,当D成立时,不难证明b与c必不平行,所以应选D.
解法二:由题设及异面直线的定义可知,若b、c都与a相交能推出b与c异面,即b与c不平行;反过来,b与c不平行不一定推出b、c都与a相交,即A是充分非必要条件,而不是充要条件,同理,B也是充分非必要条件,而非充要条件,又由b、c中至多有一条与a相交,包含b、c中有一条与a相交和b、c都不与a相交两种情形,而对于后者,即b∥a且c∥a,则b∥c.故c既非充分又非必要条件,综上所述,排除A、B、C三个选择项,从而选择D.
535. 有四个命题
(1)一条直线和另一条直线平行,它就和经过另一条直线的任何平面平行
(2)一条直线和一个平面平行,它就和这个平面内的任何直线平行
(3)平行于同一平面的两条直线平行
(4)如果直线a∥平面α,a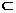 平面β,且α∩β=b,则a∥b.
平面β,且α∩β=b,则a∥b.
其中假命题共有( )
A.1个 B.2个 C.3个 D.4个
解析:此题考查线线位置关系和线面位置关系,以及空间想象能力.一条直线和另一条直线平行,它可能在经过另一条直线的平面内,故(1)是假命题.一条直线和另一个平面平行,它与这个平面的直线可能平行,也可能异面,故(2)也是假命题,又平行于同一平面的两条直线,也可能平行,也可能异面或相交,故(3)也是假命题,而命题(4)是真命题,也是线面平行的性质定理.故选C。
534. 点A为异面直线a、b外一点,过A与a、b都平行的平面( )
A.只有一个 B.只有两个
C.至多有一个 D.有无数个
解析:本题考查线线位置关系,线面位置关系,平面基本性质,以及空间想象能力
解法一:过点A作a′∥a,b′∥b,根据公理3,a′与b′确定一个平面为α,则异面直线a与b至多有一条在α内,当a、b都不在α内时,过A与a、b都平行的平面恰有一个,即α;当a、b中有一条在α内时,过A与a、b都平行的平面不存在,故选C.
解法二:过异面直线a、b分别作平面α、β使α∥β,若点A在α或β上,则过A与a、b都平行的平面不存在;若点A在α外且在β上,则过A恰有一个平面平行于α、β,则过点A与a、b都平行的平面恰有一个.
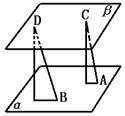
533. 已知:如图,α∥β,异面直线AB、CD和平面α、β分别交于A、B、C、D四点,E、F、G、H分别是AB、BC、CD、DA的中点,求证:(1)E、F、G、H共面;(2)面EFGH∥平面α.
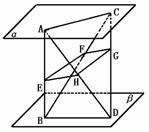
证明 (1)∵E、H分别是AB、DA的中点,∴EH∥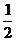 BD.同理FG∥
BD.同理FG∥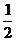 BD.∴FG∥EH.∴四边形EFGH是平行四边形,即E、F、H、G共面.
BD.∴FG∥EH.∴四边形EFGH是平行四边形,即E、F、H、G共面.
(2)平面ABD和平面α有一个公共点A,设两平面交于过点A的直线AD′∴α∥β,∴ AD′∥BD.又∵BD∥EH,∴EH∥BD∥AD′.∴EH∥平面α,EH∥平面β,同理FG∥平面α,FG∥平面β.
∴平面EFHG∥平面α∥平面β.
532. 如图,正四棱锥S-ABCD的底面边长为a,侧棱长为2a,点P、Q分别在BD和SC上,并且BP∶PD=1∶2,PQ∥平面SAD,求线段PQ的长.
解析: 要求出PQ的长,一般设法构造三角形,使PQ为其一边,然后通过解三角形的办法去处理.
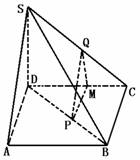
作PM∥AD交CD于M连QM,∵PM∥平面SAD,PQ∥平面SAD.
∴平面PQM∥平面SAD,而平面SCD分别与此两平行平面相交于QM,SD.
∴QM∥SD.
∵BC=a,SD=2a.
∴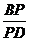 =
=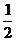 .
.
∴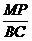 =
=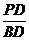 =
=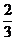 ,MP=
,MP=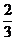 a,
a,
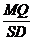 =
=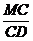 =
=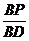 =
=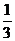 .
.
∴MQ=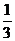 SD=
SD=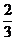 a,又∠PMQ=∠ADS.
a,又∠PMQ=∠ADS.
∴cos∠PMQ=cos∠ADS=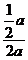 =
=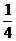 .
.
在ΔPMQ中由余弦定理得
PQ2=(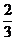 a)2+(
a)2+(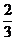 a)2-2·
a)2-2·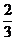 a·
a·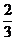 a·
a·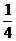 =
=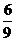 a2.
a2.
∴PQ=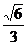 a.
a.
评析:本题的关键是运用面面平行的判定和性质,结合平行线截比例线段定理,最后由余弦定理求得结果,综合性较强.
531. 如果一条直线和两个平面中的一个相交,那么它和另一个平面也相交.
已知:α∥β,l∩α=A.
求证:l与β相交.
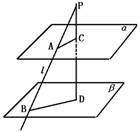
证明:∵α∥β,l∩α=A
∴A β.
β.
假设l与β不相交,则l∥β
在平面β内任取一点D,则D l.
l.
∴点D、l确定平面PBD,如图
∵α与平面PBD相交于过A的一条直线AC,
β与平面PBD相交于过点D的一条直线BD.
又α∥β ∴AC与BD无公共点.
∵AC和BD都在平面PBD内,
∴AC∥BD.
由l∥β可知l∥BD.
∴AC∥l且l与AC相交于A.
∴AC与l重合,又AC在平面α内.
∴l在α内与l∩α=A矛盾.
∴假设不成立,
∴l与β必相交.
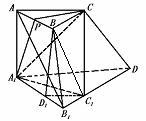
550. 三棱柱ABC-A1B1C1的侧面三条对角线AB1、BC1、CA1中,AB1⊥BC1.求证:AB1⊥CA1.
证 方法1 如图,延长B1C1到D,使C1D=B1C1.连CD、A1D.因AB1⊥BC1,故AB1⊥CD;又B1C1=A1C1=C1D,故∠B1A1D=90°,于是DA1⊥平面AA1B1B.故AB1⊥平面A1CD,因此AB1⊥A1C.
方法2 如图,取A1B1、AB的中点D1、P.连CP、C1D1、A1P、D1B,易证C1D1⊥平面AA1B1B.由三垂线定理可得AB1⊥BD1,从而AB1⊥A1D.再由三垂线定理的逆定理即得AB1⊥A1C.
说明 证明本题的关键是作辅助面和辅助线,证明线面垂直常采用下列方法:
(1)利用线面垂直的定义;(2)证明直线垂直于平面内的两条相交直线;
(3)证明直线平行于平面的垂线;(4)证明直线垂直于与这平面平行的另一平面.
549. 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F
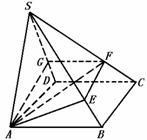 (1)求证:AF⊥SC
(1)求证:AF⊥SC
(2)若平面AEF交SD于G,求证:AG⊥SD
解析:如图,欲证AF⊥SC,只需证SC垂直于AF所在平面,即SC⊥平面AEF,由已知,欲证SC⊥平面AEF,只需证AE垂直于SC所在平面,即AE⊥平面ABC,再由已知只需证AE⊥BC,而要证AE⊥BC,只需证BC⊥平面SAB,而这可由已知得证
证明 (1)∵SA⊥平面AC,BC 平面AC,∴SA⊥BC
平面AC,∴SA⊥BC
∵矩形ABCD,∴AB⊥BC ∴BC⊥平面SAB ∴BC⊥AE又SB⊥AE ∴AE⊥平面SBC
∴SC⊥平面AEF ∴AF⊥SC
(2)∵SA⊥平面AC ∴SA⊥DC,又AD⊥DC ∴DC⊥平面SAD ∴DC⊥AG
 又由(1)有SC⊥平面AEF,AG
又由(1)有SC⊥平面AEF,AG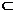 平面AEF ∴SC⊥AG ∴AG⊥平面SDC ∴AG⊥SD
平面AEF ∴SC⊥AG ∴AG⊥平面SDC ∴AG⊥SD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com