
题目列表(包括答案和解析)
518.将正方体截去一个角,求证:截面是锐角三角形.
已知:正方体中截去以P为顶点的一角得截面ABC.
求证:ΔABC是锐角三角形.
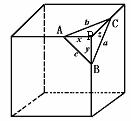
证明:如图,P-ABC是一个四面体.
∵ΔPAB、ΔPBC、ΔPCA都是直角三角形.
∴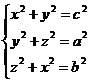 则 z2=
则 z2=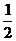 (a2+b2-c2)
(a2+b2-c2)
∵z≠0,∴a2+b2-c2>0
即 c2<a2+b2,∴b2<a2+c2.
∴∠BAC、∠ABC都小于90°.
∴ΔABC为锐角三角形.
517. 如图三棱锥P-ABC中,PA=a,AB=AC=2a,∠PAB=∠PAC=∠BAC=60°,求三棱锥P-ABC的体积.

解法一:过点P作PO⊥平面ABC于点O,∵∠PAB=∠PAC=∠BAC=60°
∴AO平分∠BAC
∴cos∠PAO=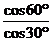 =
=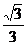 ,∴sin∠PAO=
,∴sin∠PAO= =
=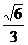
∴PO=asin∠PAO=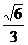 a
a
∴V棱锥=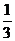 ×
×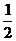 ×2a×2asin60°×
×2a×2asin60°×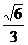 a=
a=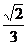 a3
a3
点评 这种方法叫直接法,就是利用锥体的体积公式直接计算,这是一种常规方法,必须掌握.
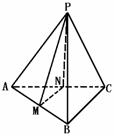
解法二:取AB、AC中点M、N的连结PM、PN
∵PA=a,AB=AC=2a,∠PAB=∠PAC=∠BAC=60°
∴三棱锥P-AMN为棱长为a的正四面体,且SΔAMN=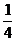 SΔABC
SΔABC
∴VP-AMN=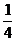 VP-ABC,而VP-AMN=
VP-ABC,而VP-AMN= a3
a3
∴VP-ABC=4VP-AMN=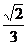 a3
a3
点评 此法是根据棱长与含有60°角的三角形的关系,把锥体截成棱长相等的三棱锥,然后根据小锥体的体积与原棱锥的体积关系,求原棱锥的体积.
解法三 在ΔPAB中,PA=a,AB=2a
又∠PAB=60°,∴∠APB=90°
同理∠APC=90°∴AP⊥平面PBC
又SΔPBC= a2 ∴VP-ABC=VA-PBC=
a2 ∴VP-ABC=VA-PBC=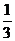 ·
· a2·a=
a2·a=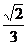 a3.
a3.
516. 在三棱锥A-BCD中,ΔABC和ΔBCD都是边长为a的正三角形,二面角A-BC-D=φ,问φ为何值时,三棱锥的全面积最大。
解析:SΔBAC=SΔBCD=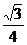 a2为常量,所以三棱锥全面积的大小取决于SΔABD与SΔACD的大小,由于ΔABD≌ΔACD,所以只求SΔACD何时面积取最大值即可。∵SΔACD=
a2为常量,所以三棱锥全面积的大小取决于SΔABD与SΔACD的大小,由于ΔABD≌ΔACD,所以只求SΔACD何时面积取最大值即可。∵SΔACD=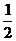 asin∠ACD,所以当∠ACD=90°时面积最大,问题得解。
asin∠ACD,所以当∠ACD=90°时面积最大,问题得解。
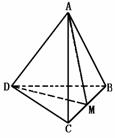
解 如图,取BC中点M,连AM、DM,∴ΔABC和ΔBCD都是正三角形,∴∠AMD是二面角A-BC-D的平面角,∠AMD=φ,又∵ΔABD≌ΔACD,且当∠ACD=90°时,ΔACD和ΔABD面积最大,此时AD= a,在ΔAMD中,由余弦定理cos∠AMD=-
a,在ΔAMD中,由余弦定理cos∠AMD=-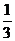 ,
,
∴当φ=π-arccos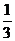 时,三棱锥A-BCD的全面积最大。
时,三棱锥A-BCD的全面积最大。
点评 本题将求棱锥全面积的最大值,转化为求ΔACD面积的最大值,间接求得φ角。
515. 正三棱锥A-BCD,底面边长为a,侧棱为2a,过点B作与侧棱AC、AD相交的截面,在这样的截面三角形中,求(1)周长的最小值;(2)周长为最小时截面积的值,(3)用这周长最小时的截面截得的小三棱锥的体积与三棱锥体积之比.
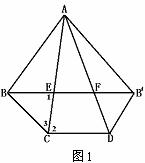
解析:(1)沿侧棱AB把正三棱锥的侧面剪开展成平面图.如图1,当周长最小时,EF在直线BB′上,∵ΔABE≌ΔB′AF,∴AE=AF,AC=AD,∴B′B∥CD,∴∠1=∠2=∠3,∴BE=BC=a,同理B′F=B′D=a.∵ΔFDB′∽ΔADB′,∴ =
=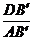 ,
,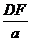 =
=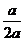 =
=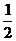 ,∴DF=
,∴DF=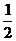 a,AF=
a,AF=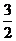 a.又∵ΔAEF∽ΔACD,∴BB′=a+
a.又∵ΔAEF∽ΔACD,∴BB′=a+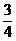 a+a=
a+a= a,∴截面三角形的周长的最小值为
a,∴截面三角形的周长的最小值为 a.
a.
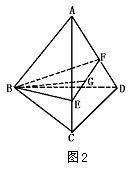
(2)如图2,∵ΔBEF等腰,取EF中点G,连BG,则BG⊥EF.∴BG=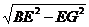 =
= =
=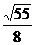 a ∴SΔBEF=
a ∴SΔBEF=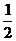 ·EF·BG=
·EF·BG=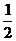 ·
·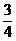 a·
a·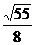 a=
a=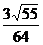 a2.
a2.
(3)∵VA-BCD=VB-ACD,而三棱锥B-AEF,三棱锥B-ACD的两个高相同,所以它们体积之比于它们的两底面积之比,即
 =
=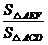 =
=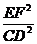 =
=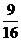
评析 把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.本题中的四面体,其中任何一个面都可以做为底面,因而它可有四个底面和与之对应的四条高,在解决有关三棱锥体积题时,需要灵活运用这个性质.
514. 已知三棱锥各侧面与底面成60°角.底面三角形的各角成等差数列,且最大边与最小边是方程3x2-21x+13=0的两根.求此三棱锥的侧面积和体积.

解析: 如图,设底面三角形的边长为a、b、c.则由条件知∠B=60°,a+c=7,ac=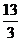 ,得b2=a2+c2-2accosB=(a+c)2-2ac(1+cosB)=72-2·
,得b2=a2+c2-2accosB=(a+c)2-2ac(1+cosB)=72-2·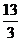 (1+
(1+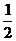 )=36
)=36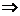 b=6,由三角形面积公式,得
b=6,由三角形面积公式,得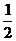 acsinB=pr(其中p为半周长,r为内切圆半径),求得r=
acsinB=pr(其中p为半周长,r为内切圆半径),求得r=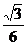 .
.
由于各侧面与底面成的角相等,∴顶点在底面上的射影是三角形的内心,且各侧面上的高相等,∴h=rtg60°=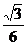 ·
·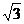 =
=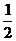 ,h侧=
,h侧= =
=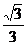 .故S侧=
.故S侧=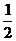 (7+6)×
(7+6)×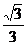 =
=
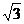 (平方单位),V=
(平方单位),V=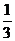 ·
·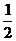 acsinBh=
acsinBh= ×
×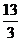 ×
×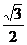 ×
×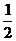 =
=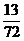
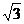 (立方单位).
(立方单位).
513. 如图,四棱锥的高为h,底面为菱形,侧面VDA和侧面VDC所成的二面角为120°,且都垂直于底面,另两个侧面与底面所成的角都是45°,求此棱锥的全面积.
解析:由面面垂直的性质可证得VD⊥底面,因为SΔVDA=SΔVDC,∠ADC=120°,DB是其平分线,而SΔVBC=SΔVAB,所以全面积不难求得.
解 由已知条件可得VD⊥底面ABCD,VD⊥DA,VD⊥DC,
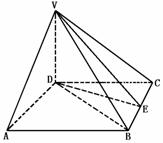
∴∠ADC=120°.
∵ABCD为菱形,
∴BD是∠ADC的平分线.
ΔADB和ΔDBC是全等的等边三角形,取BC的中点E,
连DE,BC⊥DE,BC⊥VE,∴∠VED=45°.
在直角ΔDEC中,EC=DE·ctg60°=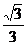 h,BC=
h,BC=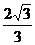 h,VE=
h,VE= h.
h.
∴S底=BC·DE=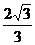 h·h=
h·h=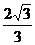 h2,
h2,
SΔVBC=SΔVAB=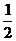 ·
·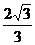 h·
h· h=
h=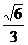 h2,
h2,
SΔVAD=SΔVDC=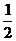 h·
h·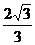 h=
h=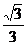 h2.
h2.
∴S全=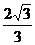 h2+
h2+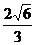 h2+
h2+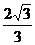 h2
h2
=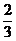 (2
(2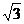 +
+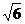 )h2
)h2
评析:本题的关键是侧面VDA和侧面VDC都垂直于底面,则它们的交线VD⊥底面ABCD,从而∠ADC=120°.
512. 以四面体各面的重心为顶点构成一个新的四面体.求这两个四面体的表面积的比.
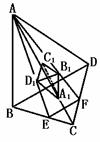
解析:因相似多面体全面积的比等于对应边的平方的比,故只须求出对应边的比.
∵B1D1=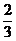 EF=
EF=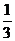 BD,
BD,
∴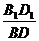 =
=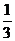 .
.
同理,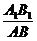 =
=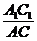 =
=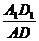 =
=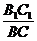 =
=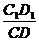 =
=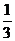 ,
,
故ABCD和A′B′C′D′是相似多面体,其表面积的比为1∶9.
511. 已知四棱锥S-ABCD的底面是边长为6的正方形,SA⊥底面ABCD,且SA=8,M是SA的中点,过M和BC作截面交SD于N.
(1)求证:截面MBCN是梯形,并求截面的面积;
(2)求截面MBCN与底面ABCD的夹角α.
解析:(1)先证MN∥BC且MN≠BC.因为BC∥AD,所以AD∥截面MBCN,从而
AD∥MN,BC∥MN.
又MN=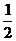 AD=
AD=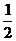 BC,所以MN≠BC.于是MN和BC平行但不相等,故MBCN是梯形.
BC,所以MN≠BC.于是MN和BC平行但不相等,故MBCN是梯形.
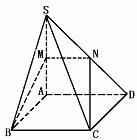
再求截面的面积:SA⊥平面ABCD.易证MN和BC都垂直于平面ABS.所以MB⊥MN,MB⊥BC,故
S截=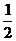 (MN+BC)·MB
(MN+BC)·MB
=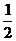 (3+6)
(3+6)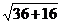 =9
=9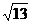 .
.
(2)首先要找到二面角的平面角.根据上面的证明,知∠MBA的是截面与底面所成二面角的平面角,即∠MBA=α.于是
tanα=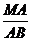 =
=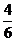 =
=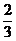
∴α=arctan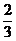
530. 已知:平面α∥平面β,且a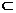 α,b
α,b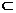 平面β,a,b为两条异面直线.
平面β,a,b为两条异面直线.
求证:异面直线a、b间的距离等于平面α,β之间的距离.
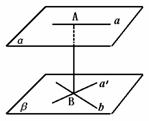
证:设AB是异面直线a、b的公垂线段,如图过点B,作直线a′,使a′∥a.
∵α∥β,a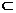 β,
β,
∴a∥β,∴a′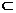 β.
β.
∵AB⊥a,∴AB⊥a′
又AB⊥b,且a′∩b=B.
∴AB⊥β
∵α∥β,∴AB⊥α
∴AB的长是平行平面α,β间的距离.
说明 求两异面直线间的距离有时可能转化为求两平行平面间的距离.
529. 已知a、b是异面直线,a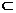 α,a∥β,b
α,a∥β,b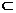 β,b∥α,求证α∥β.
β,b∥α,求证α∥β.
解析: 证明两个平面平行通常利用判定定理来证.

证明 如图,过a作任一平面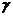 和平面β交于a′,
和平面β交于a′,
∵a∥β ∴a∥a′.
又a′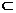 β,a′
β,a′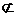 α
α
∴a′∥α且a′与b相交,
∵b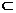 β,b∥α.
β,b∥α.
∴α∥β.
另证设c是异面直线a、b的公垂线,则过a、c可以确定一个平面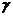 ,设γ∩β=a′∵a∥β,∴a′∥a,
,设γ∩β=a′∵a∥β,∴a′∥a,
∵c⊥a,∴c⊥a′又∵c⊥b,a′,b相交,∴c⊥β
同理可证:c⊥α,∴α∥β
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com