
题目列表(包括答案和解析)
2、设数列{an}的前n项和为Sn,Sn= (对于所有n≥1),且a4=54,则a1的数值是_____.
(对于所有n≥1),且a4=54,则a1的数值是_____.
1、在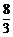 和
和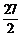 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为_____.
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为_____.
6、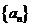 是首项
是首项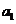 =1,公差为
=1,公差为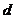 =3的等差数列,如果
=3的等差数列,如果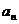 =2005,则序号
=2005,则序号 等于
( )
等于
( )
A 667 B 668 C 669 D 670
5、已知由正数组成的等比数列{an}中,公比q=2, a1·a2·a3·…·a30=245, 则a1·a4·a7·…·a28= ( ) A 25 B 210 C 215 D 220
4、如果数列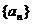 是等差数列,则 ( )
是等差数列,则 ( )
A
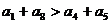 B
B
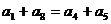
C 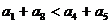 D
D
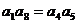
3、已知等差数列 的公差为2,若
的公差为2,若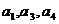 成等比数列, 则
成等比数列, 则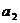 = ( )
= ( )
A –4 B –6 C –8 D –10
2、在各项都为正数的等比数列{an}中,首项a1=3 ,前三项和为21,则a3+ a4+ a5=( )
A 33 B 72 C 84 D 189
1、 已知等差数列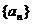 中,
中,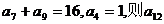 的值是 ( )
的值是 ( )
A 15 B 30 C 31 D 64
2、解:(1)∵AD=2AB=2,E是AD的中点,
∴△BAE,△CDE是等腰直角三角形,
易知, ∠BEC=90°,即BE⊥EC.
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又C D′Ì 面D′EC , ∴BE⊥CD′;
(2)法一:设M是线段EC的中点,过M作MF⊥BC
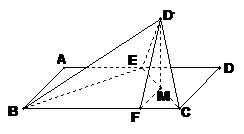 垂足为F,连接D′M,D′F,则D′M⊥EC.
垂足为F,连接D′M,D′F,则D′M⊥EC.
∵平面D′EC⊥平面BEC,
∴D′M⊥平面EBC,
∴MF是D′F在平面BEC上的射影,由三垂线定理得:
D′F⊥BC
∴∠D′FM是二面D′-BC-E的平面角.
在Rt△D′MF中,D′M=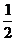 EC=
EC=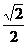 ,MF=
,MF=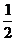 AB=
AB=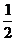
∴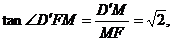
即二面角D′-BC-E的正切值为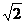 .
.
法二:如图,以EB,EC为x轴、y轴,过E垂直于平面BEC的射线为z轴,建立空间直角坐标系.
则B(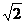 ,0,0),C(0,
,0,0),C(0,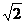 ,0),D′(0,
,0),D′(0,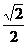 ,
,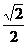 )
)
设平面BEC的法向量为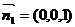 ;平面D′BC的法向量为
;平面D′BC的法向量为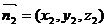
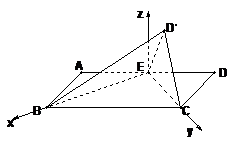
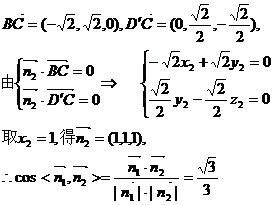
Þ tan = ∴二面角D′-BC-E的正切值为
= ∴二面角D′-BC-E的正切值为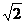 .
.
1、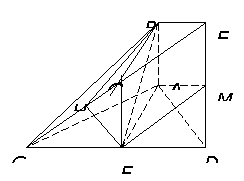 方法一:
方法一:
(1) 证法一:取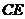 的中点
的中点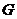 ,连
,连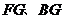 .
.
∵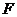 为
为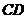 的中点,∴
的中点,∴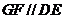 且
且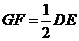 . …………1分
. …………1分
∵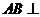 平面
平面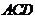 ,
,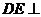 平面
平面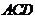 ,
,
∴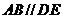 ,∴
,∴ .
…………2分
.
…………2分
又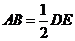 ,∴
,∴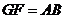 .
…………3分
.
…………3分
∴四边形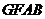 为平行四边形,则
为平行四边形,则 . …………4分
. …………4分
∵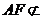 平面
平面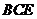 ,
,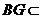 平面
平面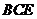 ,
,
∴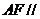 平面
平面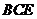 .
…………5分
.
…………5分
证法二:取 的中点
的中点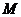 ,连
,连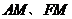 .
.
∵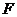 为
为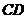 的中点,∴
的中点,∴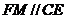 .
…………1分
.
…………1分
∵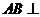 平面
平面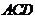 ,
,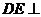 平面
平面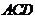 ,∴
,∴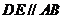 .
…………2分
.
…………2分
又 ,
,
∴四边形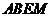 为平行四边形,则
为平行四边形,则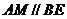 .
…………3分
.
…………3分
∵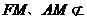 平面
平面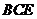 ,
,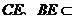 平面
平面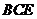 ,
,
∴ 平面
平面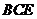 ,
,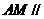 平面
平面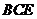 .
.
又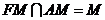 ,∴平面
,∴平面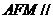 平面
平面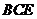 .
…………4分
.
…………4分
∵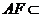 平面
平面 ,
,
∴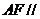 平面
平面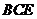 .
…………5分
.
…………5分
(2) 证:∵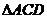 为等边三角形,
为等边三角形,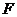 为
为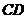 的中点,∴
的中点,∴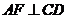 . …………6分
. …………6分
∵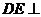 平面
平面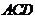 ,
,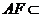 平面
平面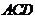 ,∴
,∴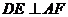 . …………7分
. …………7分
又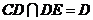 ,故
,故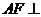 平面
平面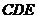 .
…………8分
.
…………8分
∵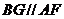 ,∴
,∴ 平面
平面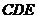 .
…………9分
.
…………9分
∵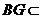 平面
平面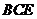 ,
,
∴平面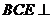 平面
平面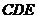 .
…………10分(3)
.
…………10分(3)
解:在平面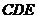 内,过
内,过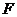 作
作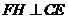 于
于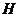 ,连
,连 .
.
∵平面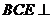 平面
平面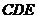 , ∴
, ∴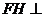 平面
平面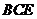 .
.
∴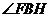 为
为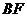 和平面
和平面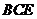 所成的角.
…………12分
所成的角.
…………12分
设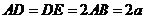 ,则
,则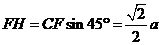 ,
,
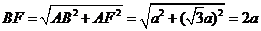 ,
,
R t△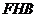 中,
中,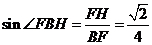 .
.
 ∴直线
∴直线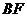 和平面
和平面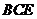 所成角的正弦值为
所成角的正弦值为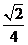 . …………14分
. …………14分
方法二:
设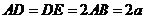 ,建立如图所示的坐标系
,建立如图所示的坐标系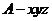 ,则
,则
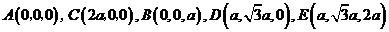 .…………2分
.…………2分
∵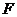 为
为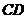 的中点,∴
的中点,∴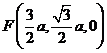 .
…………3分
.
…………3分
(1) 证: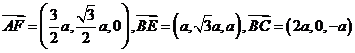 , …………4分
, …………4分
∵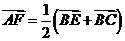 ,
,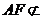 平面
平面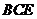 ,∴
,∴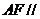 平面
平面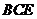 . …………5分
. …………5分
(2) 证:∵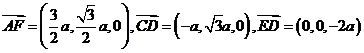 ,
…………6分
,
…………6分
∴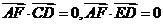 ,∴
,∴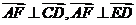 . …………8分
. …………8分
∴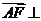 平面
平面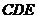 ,又
,又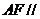 平面
平面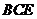 ,
,
∴平面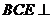 平面
平面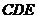 . …………10分
. …………10分
(3) 解:设平面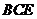 的法向量为
的法向量为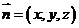 ,由
,由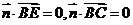 可得:
可得:
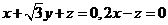 ,取
,取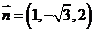 . …………12分
. …………12分
又 ,设
,设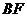 和平面
和平面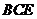 所成的角为
所成的角为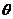 ,则
,则
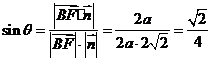 .
.
∴直线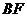 和平面
和平面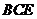 所成角的正弦值为
所成角的正弦值为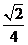 .
…………14分
.
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com