
题目列表(包括答案和解析)
令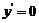 ,即
,即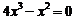 ,解得
,解得 ,
,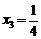 .
.
当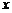 变化时,
变化时, ,
,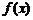 的变化情况如下表:
的变化情况如下表:
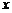 |
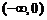 |
0 |
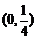 |
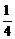 |
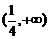 |
 |
- |
0 |
- |
0 |
+ |
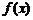 |
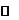 |
/ |
 |
极小值 |
 |
因此,当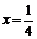 时,
时,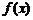 有极小值,且
有极小值,且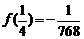 .
.
2、解:联立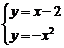 ,得
,得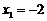 ,
,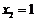 .
.
所以,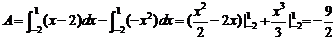 ,故所求面积
,故所求面积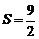 .
.
4、解: .
.
令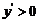 ,即
,即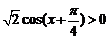 ,解得
,解得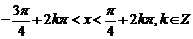 ;
;
令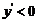 ,即
,即 ,解得
,解得 .
.
故函数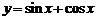 的单调增区间为
的单调增区间为 ;单调减区间为
;单调减区间为
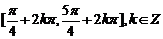 .
.
3、做一个体积为32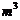 ,高为2
,高为2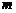 的长方体纸盒(1)若用
的长方体纸盒(1)若用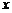 表示长方体底面一边的长,
表示长方体底面一边的长,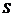 表示长方体的侧面积,试写出
表示长方体的侧面积,试写出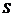 与
与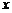 间的函数关系式;(2)当
间的函数关系式;(2)当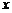 取什么值时,做一个这样的长方体纸盒用纸最少?
取什么值时,做一个这样的长方体纸盒用纸最少?
高三数学章节训练题8《导数及其应用练习题2》
2、求由直线 和曲线
和曲线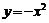 所围成的图形的面积.
所围成的图形的面积.
1、求函数 的极值.
的极值.
4.函数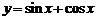 的单调区间
的单调区间
3. 函数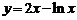 的递减区间是 .
的递减区间是 .
2. 曲线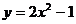 在点(
在点(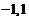 )的切线方程为 .
)的切线方程为 .
1. 若函数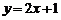 ,则
,则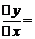 .
.
6. ( )
( )
A.1 B. C.-
C.- D.-1
D.-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com