
题目列表(包括答案和解析)
1. 已知函数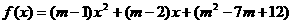 为偶函数,则
为偶函数,则 的值是( )
的值是( )
A. 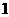 B.
B. 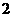 C.
C. 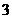 D.
D. 
12.
[解析]:(Ⅰ)直线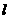 的方程为
的方程为 ,将
,将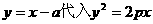 ,
,
得  . 设直线
. 设直线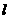 与抛物线两个不同交点的坐标为
与抛物线两个不同交点的坐标为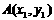 、
、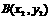 ,
,
则 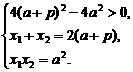 又
又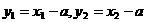 ,
,
∴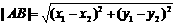
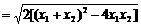
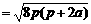 . ∵
. ∵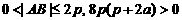 , ∴
, ∴  . 解得
. 解得
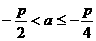 .
.
(Ⅱ)设AB的垂直平分线交AB于点Q,令坐标为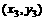 ,则由中点坐标公式,得
,则由中点坐标公式,得
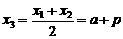 ,
,
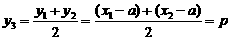 .
.
∴ 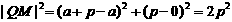 . 又
. 又  为等腰直角三角形,
为等腰直角三角形,
∴ 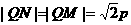 , ∴
, ∴
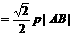

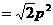
即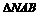 面积最大值为
面积最大值为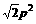
11.[解析]:设抛物线方程为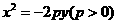 ,则焦点F(
,则焦点F(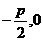 ),由题意可得
),由题意可得
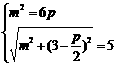 ,解之得
,解之得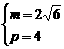 或
或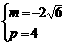 ,
,
故所求的抛物线方程为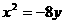 ,
,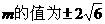
10.1米. 由题意知,设抛物线的方程为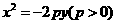 ,又抛物线的跨度为16,拱高为4,所以点(8,-4)为抛物线上的点,所以
,又抛物线的跨度为16,拱高为4,所以点(8,-4)为抛物线上的点,所以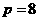 .即抛物线方程为
.即抛物线方程为 .所以当
.所以当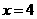 时,
时,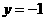 ,所以柱子的高度为1米.
,所以柱子的高度为1米.
9.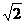 [思路分析]:
[思路分析]: 的准线是
的准线是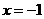 . ∴
. ∴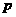 到
到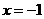 的距离等于
的距离等于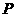 到焦点
到焦点 的距离,故点
的距离,故点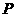 到点
到点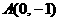 的距离与
的距离与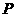 到
到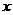 =
=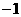 的距离之和的最小值为
的距离之和的最小值为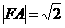 .
.
[命题分析]:考查圆锥曲线的定义及数形结合,化归转化的思想方法.
8.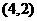
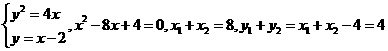
中点坐标为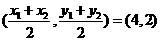
7. 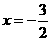
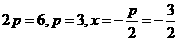
6.A 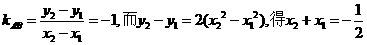 ,且
,且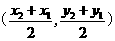
在直线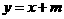 上,即
上,即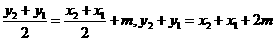
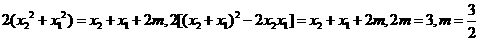
5.C
[思路分析]:由于点P到准线的距离等于点P到焦点F的距离,所以过焦点F到直线x+2y+10=0的距离即是
[命题分析]:考察抛物线的几何性质及距离的转化思想
4.D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com