
题目列表(包括答案和解析)
7、(2009宣威六中第一次月考)已知数列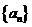 满足
满足
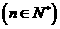 ,且
,且
(1)用数学归纳法证明: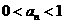 ;
;
(2)若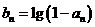 ,且
,且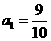 ,求无穷数列
,求无穷数列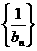 所有项的和。
所有项的和。
解:

6、(2009广州一模)已知数列{an}的相邻两项an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,且a1=1.
(1)求证:数列{
an-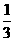 ×2n}是等比数列;
×2n}是等比数列;
(2)设Sn是数列{an}的前n项的和,问是否存在常数λ,使得bn-λSn>0对任意n∈N*都成立,若存在,求出λ的取值范围;若不存在,请说明理由.
(本题主要考查数列的通项公式、数列前n项和、不等式等基础知识,考查化归与转化、分类与整合、特殊与一般的数学思想方法,以及推理论证能力、运算求解能力和抽象概括能力)
(1)证法1:∵an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,
∴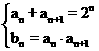 ……2分
……2分
由an+an+1=2n,得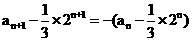 ,故数列
,故数列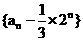
是首项为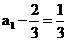 ,公比为-1的等比数列.
……4分
,公比为-1的等比数列.
……4分
证法2:∵an,an+1是关于x 的方程x2-2n x+ bn=0 (n∈N*)的两根,
∴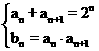 ……2分
……2分
∵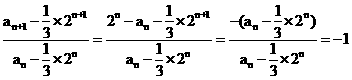 ,
,
故数列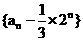 是首项为
是首项为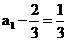 ,公比为-1的等比数列.
,公比为-1的等比数列.
……4分
(2)解:由(1)得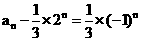 ,即
,即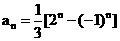 ,
,
∴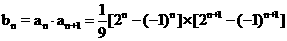
 ……6分
……6分
∴Sn=a1+
a2+ a3+…+ an=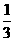 [(2+22+23+…+2n)-[(-1)+ (-1)2+…+(-1)n]
[(2+22+23+…+2n)-[(-1)+ (-1)2+…+(-1)n]
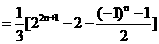 ,
……8分
,
……8分
要使得bn-λSn>0对任意n∈N*都成立,
即 对任意n∈N*都成立.
对任意n∈N*都成立.
①当n为正奇数时,由(*)式得 ,
,
即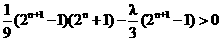 ,
,
∵2n+1-1>0,∴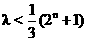 对任意正奇数n都成立.
对任意正奇数n都成立.
当且仅当n=1时,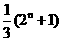 有最小值1,∴λ<1. ……10分
有最小值1,∴λ<1. ……10分
①当n为正奇数时,由(*)式得 ,
,
即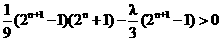 ,
,
∵2n+1-1>0,∴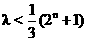 对任意正奇数n都成立.
对任意正奇数n都成立.
当且仅当n=1时,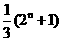 有最小值1,∴λ<1.
……10分
有最小值1,∴λ<1.
……10分
②当n为正偶数时,由(*)式得 ,
,
即 ,
,
∵2n-1>0,∴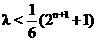 对任意正偶数n都成立.
对任意正偶数n都成立.
当且仅当n=2时, 有最小值1.5,∴λ<1.5.
……12分
有最小值1.5,∴λ<1.5.
……12分
综上所述,存在常数λ,使得bn-λSn>0对任意n∈N*都成立,λ的取值范围是(-∞,1).
……14分
5、(2009上海八校联考)已知点列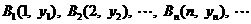
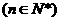 顺次为直线
顺次为直线 上的点,点列
上的点,点列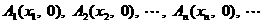
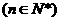 顺次为
顺次为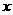 轴上的点,其中
轴上的点,其中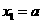
 ,对任意的
,对任意的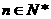 ,点
,点 、
、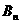 、
、 构成以
构成以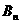 为顶点的等腰三角形。
为顶点的等腰三角形。
(1)证明:数列 是等差数列;
是等差数列;
(2)求证:对任意的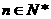 ,
, 是常数,并求数列
是常数,并求数列 的通项公式;
的通项公式;
(3)对上述等腰三角形 添加适当条件,提出一个问题,并做出解答。
添加适当条件,提出一个问题,并做出解答。
(根据所提问题及解答的完整程度,分档次给分)
解: (1)依题意有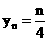 ,于是
,于是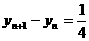 .
.
所以数列 是等差数列.
是等差数列.
 .4分
.4分
(2)由题意得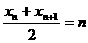 ,即
,即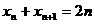 , (
, ( )
①
)
①
所以又有 .
②
.
②
由②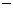 ①得:
①得: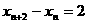 , 所以
, 所以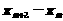 是常数.
是常数.  6分
6分
由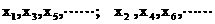 都是等差数列.
都是等差数列.
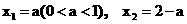 ,那么得
,那么得 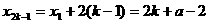 ,
,
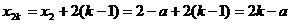 . (
. (


 8分
8分
故
 10分
10分
(3) 提出问题①:若等腰三角形 中,是否有直角三角形,若有,求出实数
中,是否有直角三角形,若有,求出实数
提出问题②:若等腰三角形 中,是否有正三角形,若有,求出实数
中,是否有正三角形,若有,求出实数
解:问题①  11分
11分
当 为奇数时,
为奇数时, ,所以
,所以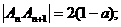
当 为偶数时,
为偶数时,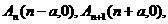 所以
所以
作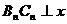 轴,垂足为
轴,垂足为 则
则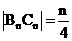 ,要使等腰三角形
,要使等腰三角形 为直角三角形,必须且只须:
为直角三角形,必须且只须: .
.
 13分
13分
当 为奇数时,有
为奇数时,有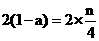 ,即
,即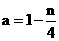 ①
①
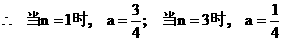 , 当
, 当 ,
,  不合题意.
不合题意. 15分
15分
当 为偶数时,有
为偶数时,有 ,
,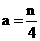 ,同理可求得
,同理可求得

当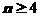 时,
时, 不合题意.
不合题意.  17分
17分
综上所述,使等腰三角形 中,有直角三角形,
中,有直角三角形,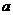 的值为
的值为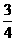 或
或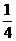 或
或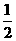 .
.
 18分
18分
解:问题②  11分
11分
当 为奇数时,
为奇数时, ,所以
,所以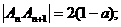
当 为偶数时,
为偶数时,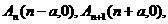 所以
所以
作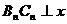 轴,垂足为
轴,垂足为 则
则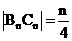 ,要使等腰三角形
,要使等腰三角形 为正三角形,必须且只须:
为正三角形,必须且只须: .
.
 13分
13分
当 为奇数时,有
为奇数时,有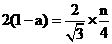 ,即
,即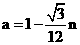 ①
①
 , 当
, 当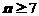 时,.
时,.  不合题意.
不合题意.  15分
15分
当 为偶数时,有
为偶数时,有 ,
,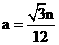 ,同理可求得
,同理可求得
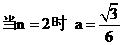 .
.
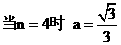 ;
;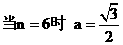 ;当
;当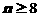 时,
时, 不合题意.
不合题意. 17分
17分
综上所述,使等腰三角形 中,有正三角形,
中,有正三角形,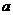 的值为
的值为
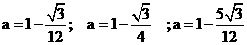 ;
;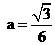 ;
;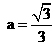 ;
;
 18分
18分
4、(2009上海青浦区)设数列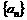 的前
的前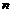 和为
和为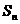 ,已知
,已知 ,
,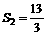 ,
, ,
,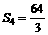 ,
,
一般地, (
( ).
).
(1)求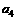 ;
;
(2)求 ;
;
(3)求和: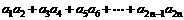 .
.
(1)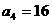 ;
……3分
;
……3分
(2)当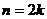 时,(
时,( )
)
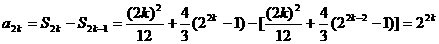 , ……6分
, ……6分
所以,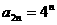 (
(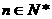 ).
……8分
).
……8分
(3)与(2)同理可求得: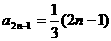 ,
……10分
,
……10分
设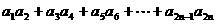 =
=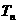 ,
,
则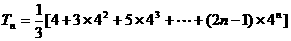 ,(用等比数列前n项和公式的推导方法)
,(用等比数列前n项和公式的推导方法) ,相减得
,相减得
 ,所以
,所以
 .
……14分
.
……14分
即- <λ<1,又λ≠0,λ为整数,
<λ<1,又λ≠0,λ为整数,
∴λ=-1,使得对任意n∈N*,都有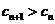 . 12分
. 12分
3、(2009台州市第一次调研)已知数列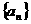 的首项
的首项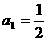 ,前n项和
,前n项和 .
.
(Ⅰ)求证: ;
;
(Ⅱ)记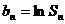 ,
,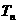 为
为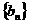 的前n项和,求
的前n项和,求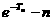 的值.
的值.
解:(1)由 ①,得
①,得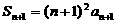 ②,
②,
②-①得: . 4分
. 4分
(2)由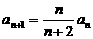 求得
求得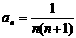 . 7分
. 7分
∴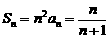 ,
,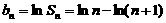 11分
11分
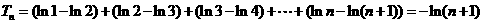
∴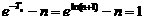 .
14分
.
14分
2、(2009滨州一模)已知曲线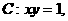 过
过 上一点
上一点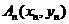 作一斜率为
作一斜率为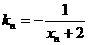 的直线交曲线
的直线交曲线 于另一点
于另一点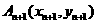 ,点列
,点列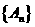 的横坐标构成数列
的横坐标构成数列 ,其中
,其中 .
.
(I)求 与
与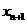 的关系式;
的关系式;
(II)令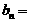
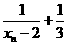 ,求证:数列
,求证:数列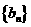 是等比数列;
是等比数列;
(III)若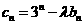 (λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立。
(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立。
(1) 解:过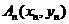 的直线方程为
的直线方程为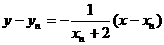
联立方程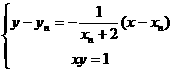 消去
消去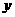 得
得
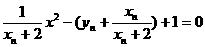
∴
即
(2)
∴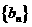 是等比数列
是等比数列
 ,
,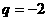 ;
;
(III) 由(II)知,
由(II)知,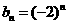 ,要使
,要使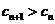 恒成立由
恒成立由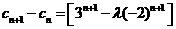
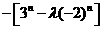 =
=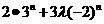 >0恒成立,
>0恒成立,
即(-1)nλ>-( )n-1恒成立.
)n-1恒成立.
ⅰ。当n为奇数时,即λ<( )n-1恒成立.
)n-1恒成立.
又( )n-1的最小值为1.∴λ<1. 10分
)n-1的最小值为1.∴λ<1. 10分
ⅱ。当n为偶数时,即λ>-( )n-1恒成立,
)n-1恒成立,
1、(2009杭州二中第六次月考)数列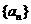 中,
中, 其中
其中 且
且 ,
,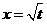 是函数
是函数
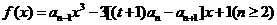 的一个极值点.
的一个极值点.
(Ⅰ)证明: 数列 是等比数列;
是等比数列;
(Ⅱ)求 .
.
(1)由题意得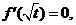 即
即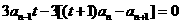 ,
,
 ,
,
 当
当 时,数列
时,数列 是以
是以 为首项,
为首项,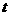 为公比的等比数列,
为公比的等比数列,
(2) 即
即

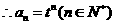 ,此式对
,此式对 也成立.
也成立.
4、(2009宁波十校联考)已知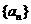 是等差数列,
是等差数列, ,则该数列前10项和
,则该数列前10项和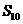 =________
=________
答案 100
3、(2009江门一模)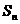 是等差数列
是等差数列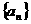 的前
的前 项和,若
项和,若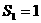 ,
,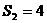 ,
,
则 .
.
答案 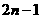
2、(2009上海八校联考)在数列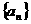 中,
中,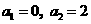 ,且
,且 ,
, _________。
_________。
答案 2550
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com