
题目列表(包括答案和解析)
6.(2009宜春)在等差数列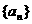 中,
中, ,
,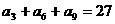 ,则数列
,则数列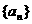 的前9项之和
的前9项之和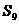 等于 ( )
等于 ( )
A.66 B.99 C.144 D..297
答案 B
5.(2009长沙一中期末)各项不为零的等差数列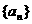 中,
中,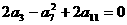 ,则
,则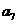 的值为 ( )
的值为 ( )
A. B.4 C.
B.4 C. D.
D.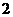
答案 B
4.(2009厦门一中文)在等差数列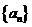 中,
中,
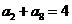 ,则 其前9项的和S9等于 ( )
,则 其前9项的和S9等于 ( )
A.18 B 27 C 36 D 9
答案 A
3.(2009福州三中)已知等差数列{an}的前n项和为Sn,若 ,则
,则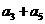 的值为( )
的值为( )
A.2 B.4 C.7 D.8
答案 B
2. (北京市西城区2009年4月高三一模抽样测试理) 若数列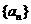 是公比为4的等比数列,且
是公比为4的等比数列,且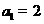 ,则数列
,则数列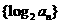 是( )
是( )
A. 公差为2的等差数列
B. 公差为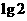 的等差数列
的等差数列
C. 公比为2的等比数列
D. 公比为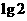 的等比数列
的等比数列
答案 A
1.(北京市朝阳区2009年4月高三一模理)各项均不为零的等差数列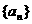 中,若
中,若 ,则
,则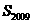 等于 ( )
等于 ( )
A.0 B.2 C.2009 D.4018
答案 D
11、(2009深圳一模文)设数列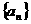 的前
的前 项和为
项和为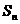 ,
,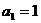 ,且对任意正整数
,且对任意正整数 ,点
,点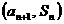 在直线
在直线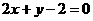 上.
上.
(Ⅰ) 求数列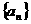 的通项公式;
的通项公式;
(Ⅱ)是否存在实数 ,使得数列
,使得数列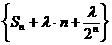 为等差数列?若存在,求出
为等差数列?若存在,求出 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
(Ⅲ)求证: 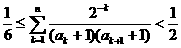 .
.
解:(Ⅰ)由题意可得:
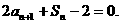 ①
①
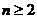 时,
时, 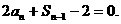 ②
…………………… 1分
②
…………………… 1分
①─②得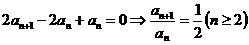 ,
, 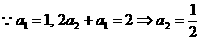 …………………… 3分
…………………… 3分

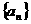 是首项为
是首项为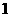 ,公比为
,公比为 的等比数列,
的等比数列,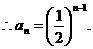 ……………… 4分
……………… 4分
(Ⅱ)解法一: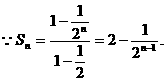 ………………
5分
………………
5分
若 为等差数列,
为等差数列,
则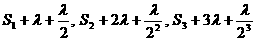 成等差数列, ……………… 6分
成等差数列, ……………… 6分
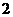
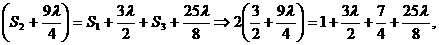
得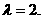 ………………
8分
………………
8分
又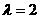 时,
时,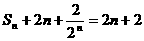 ,显然
,显然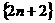 成等差数列,
成等差数列,
故存在实数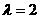 ,使得数列
,使得数列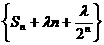 成等差数列. ……………… 9分
成等差数列. ……………… 9分
解法二: 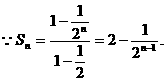 ……………… 5分
……………… 5分
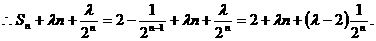 …………… 7分
…………… 7分
欲使 成等差数列,只须
成等差数列,只须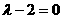 即
即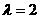 便可. ……………8分
便可. ……………8分
故存在实数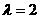 ,使得数列
,使得数列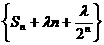 成等差数列. ……………… 9分
成等差数列. ……………… 9分
(Ⅲ)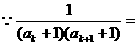
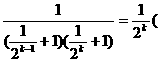
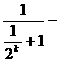
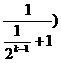 …… 10分
…… 10分
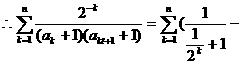
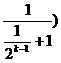 …………
11分
…………
11分

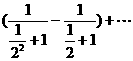

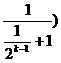
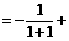
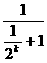
 ………… 12分
………… 12分
又函数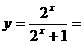
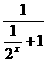 在
在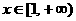 上为增函数,
上为增函数,
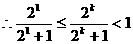 ,
…………
13分
,
…………
13分
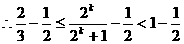 ,
,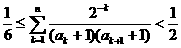 . ……… 14分
. ……… 14分
2009年联考题
10、(2009汕头一模)在等比数列{an}中,an>0 (n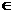 N*),公比q
N*),公比q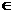 (0,1),且a1a5
+ 2a3a5 +a 2a8=25,
(0,1),且a1a5
+ 2a3a5 +a 2a8=25,
a3与as的等比中项为2。
(1)求数列{an}的通项公式;
(2)设bn=log2
an,数列{bn}的前n项和为Sn当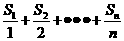 最大时,求n的值。
最大时,求n的值。
解:(1)因为a1a5
+ 2a3a5 +a 2a8=25,所以,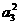 + 2a3a5
+
+ 2a3a5
+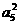 =25
=25
又an>o,…a3+a5=5,…………………………2分
又a3与a5的等比中项为2,所以,a3a5=4
而q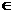 (0,1),所以,a3>a5,所以,a3=4,a5=1,
(0,1),所以,a3>a5,所以,a3=4,a5=1,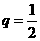 ,a1=16,所以,
,a1=16,所以,
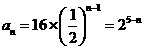 …………………………6分
…………………………6分
(2)bn=log2 an=5-n,所以,bn+1-bn=-1,
所以,{bn}是以4为首项,-1为公差的等差数列。。。。。。。。。9分
所以,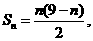
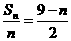
所以,当n≤8时,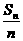 >0,当n=9时,
>0,当n=9时,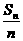 =0,n>9时,
=0,n>9时,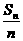 <0,
<0,
当n=8或9时,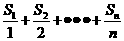 最大。 …………………………12分
最大。 …………………………12分
9、(2009江门一模)已知等差数列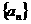 和正项等比数列
和正项等比数列 ,
,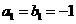 ,
,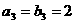 .
.
⑴求 、
、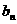 ;
;
⑵对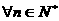 ,试比较
,试比较 、
、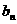 的大小;
的大小;
⑶设 的前
的前 项和为
项和为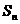 ,是否存在常数
,是否存在常数 、
、 ,使
,使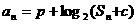 恒成立?若存在,求
恒成立?若存在,求 、
、 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:⑴由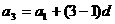 ,得
,得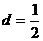 -------1分 由
-------1分 由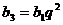 且
且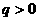 得
得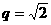 ----2分
----2分
所以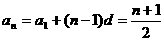 ,
,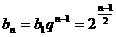 -------4分
-------4分
⑵显然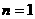 ,
,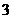 时,
时,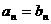 ;
;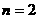 时,
时,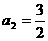 ,
,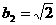 ,
,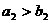 -------5分
-------5分
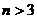 时,
时,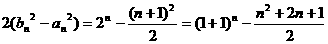
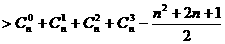 -------6分
-------6分 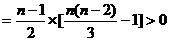 -------7分
-------7分
因为 、
、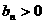 ,所以
,所以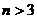 时,
时,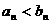 -------8分
-------8分
⑶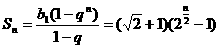 -------9分,
-------9分,
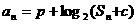 恒成立,则有
恒成立,则有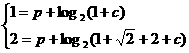 -------11分,解得
-------11分,解得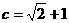 ,
,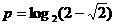 -------12分
-------12分
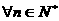 ,
,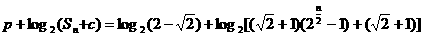
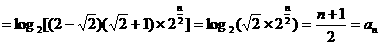 -------13分
-------13分
所以,当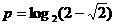 ,
,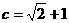 时,
时,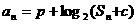 恒成立-------14分
恒成立-------14分
8、(2009广东三校一模)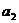 ,
, 是方程
是方程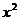
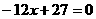 的两根,数列
的两根,数列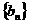 的前
的前 项和为
项和为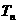 ,且
,且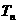
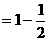
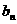
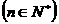
(1)求数列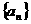 ,
,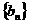 的通项公式;
的通项公式;
(2)记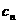 =
=
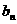 ,求数列
,求数列 的前
的前 项和
项和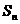 .
.
解:(1)由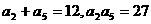 .且
.且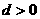 得
得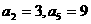 2分
2分
 ,
,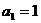
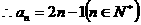 4分
4分
在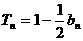 中,令
中,令 得
得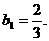 当
当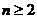 时,T
时,T =
=
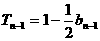 ,
,
两式相减得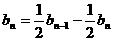 ,
,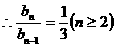 6分
6分
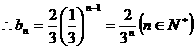 .
8分
.
8分
(2)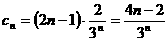 , 9分
, 9分
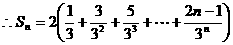 ,
,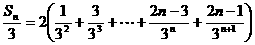 , 10分
, 10分
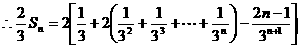 =2
=2
=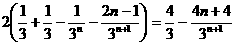 ,
13分
,
13分
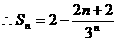 14分
14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com