
题目列表(包括答案和解析)
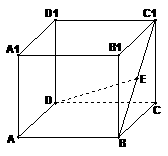
5、(2009东莞一模)如图,在长方体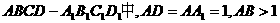 ,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为
,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为 .
.
 (1)求证:D1E⊥A1D;
(1)求证:D1E⊥A1D;
(2)求AB的长度;
(3)在线段AB上是否存在点E,使得二面角
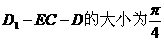 。若存在,确定
。若存在,确定
点E的位置;若不存在,请说明理由.
解一:(1)证明:连结AD1,由长方体的性质可知:
 AE⊥平面AD1,∴AD1是ED1在
AE⊥平面AD1,∴AD1是ED1在
平面AD1内的射影。又∵AD=AA1=1,
∴AD1⊥A1D
∴D1E⊥A1D1(三垂线定理) 4分
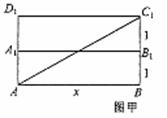
(2)设AB=x,∵四边形ADD1A是正方形,
∴小蚂蚁从点A沿长方体的表面爬到
 点C1可能有两种途径,如图甲的最短路程为
点C1可能有两种途径,如图甲的最短路程为
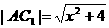
如图乙的最短路程为
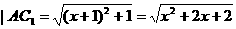


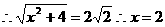 ………………9分
………………9分
(3)假设存在,平面DEC的法向量 ,
,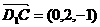
设平面D1EC的法向量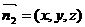 ,则
,则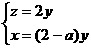
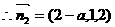 …………………12分
…………………12分
由题意得: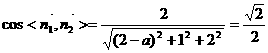
解得: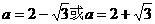 (舍去)
(舍去)
 ………14分
………14分
2009年联考题
4. (2009闸北区) 如图,在四棱锥 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,
, ,
, 为
为 的中点.
的中点.
 (Ⅰ)求四棱锥
(Ⅰ)求四棱锥 的体积;
的体积;
(Ⅱ)求异面直线OB与MD所成角的大小.
解:(Ⅰ)由已知可求得,正方形 的面积
的面积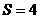 ,……………………………2分
,……………………………2分
所以,求棱锥 的体积
的体积 ………………………………………4分
………………………………………4分
(Ⅱ)方法一(综合法)
设线段 的中点为
的中点为 ,连接
,连接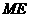 ,
,
则 为异面直线OC与
为异面直线OC与 所成的角(或其补角) ………………………………..1分
所成的角(或其补角) ………………………………..1分
由已知,可得 ,
,
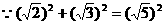
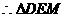 为直角三角形 …………………………………………………………….2分
为直角三角形 …………………………………………………………….2分
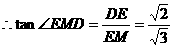 , …………………………………………………………….4分
, …………………………………………………………….4分
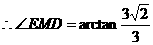 .
.
所以,异面直线OC与MD所成角的大小 . …………………..1分
. …………………..1分
方法二(向量法)
以AB,AD,AO所在直线为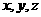 轴建立坐标系,
轴建立坐标系,
则 , ………………………………………………2分
, ………………………………………………2分
 ,
, ,
…………………………………………………………………………..2分
,
…………………………………………………………………………..2分
设异面直线OC与MD所成角为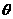 ,
,
 .……………………………………3分
.……………………………………3分
 OC与MD所成角的大小为
OC与MD所成角的大小为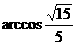 .……………………………………………1分
.……………………………………………1分
3.(2009冠龙高级中学3月月考)在棱长为2的正方体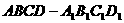 中,(如图)
中,(如图)

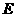 是棱
是棱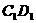 的中点,
的中点,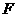 是侧面
是侧面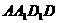 的中心.
的中心.
(1) 求三棱锥 的体积;
的体积;
求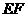 与底面
与底面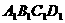 所成的角的大小.(结果用反三角函数表示)
所成的角的大小.(结果用反三角函数表示)
(1)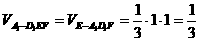 .
.
 (2)取
(2)取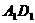 的中点
的中点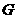 ,所求的角的大小等于
,所求的角的大小等于 的大小,
的大小,
 中
中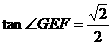 ,所以
,所以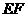 与底面
与底面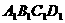 所成的角的大小是
所成的角的大小是 .
.
2.(2009上海奉贤区模拟考)在直三棱柱ABC-A1B1C1中,∠ABC=90°, AB=BC=1.
(1)求异面直线B1C1与AC所成角的大小;
(2)若直线A1C与平面ABC所成角为45°,
求三棱锥A1-ABC的体积.
(1)因为 ,所以∠BCA(或其补角)即为异面直线
,所以∠BCA(或其补角)即为异面直线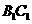 与
与 所成角
-------(3分)
所成角
-------(3分)
∠ABC=90°, AB=BC=1,所以 , -------(2分)
, -------(2分)
即异面直线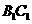 与
与 所成角大小为
所成角大小为 。 -------(1分)
。 -------(1分)
(2)直三棱柱ABC-A1B1C1中,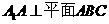 ,所以
,所以 即为直线A1C与平面ABC所成角,所以
即为直线A1C与平面ABC所成角,所以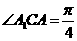 。 -------(2分)
。 -------(2分)
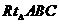 中,AB=BC=1得到
中,AB=BC=1得到 ,
,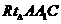 中,得到
中,得到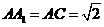 , ------(2分)
, ------(2分)
所以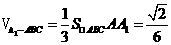 -------(2分)
-------(2分)
1.(2009上海普陀区)已知复数 ,
,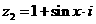 (
(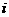 是虚数单位),且
是虚数单位),且 .当实数
.当实数 时,试用列举法表示满足条件的
时,试用列举法表示满足条件的 的取值集合
的取值集合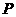 .
.
解:如图,设 中点为
中点为 ,联结
,联结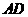 、
、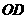 .
.
由题意, ,
, ,所以
,所以 为等边三角形,
为等边三角形,
故 ,且
,且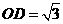 .
.
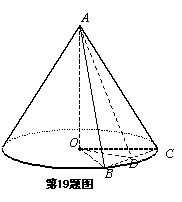 又
又 ,
,
所以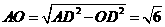 .
.
而圆锥体的底面圆面积为 ,
,
所以圆锥体体积 .
.
2.(2009上海青浦区)如图,用一平面去截球所得截面的面积为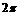 cm2,已知
cm2,已知
球心到该截面的距离为1 cm,则该球的体积是 cm3.
答案 
1. (2009上海八校联考)已知一个球的球心
(2009上海八校联考)已知一个球的球心 到过球面上A、B、C三点的截面的距离等于此球半径的一半,若
到过球面上A、B、C三点的截面的距离等于此球半径的一半,若 ,则球的体积为________________。
,则球的体积为________________。
答案

9.(2009番禺一模)一个几何体的三视图如右图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为( ).
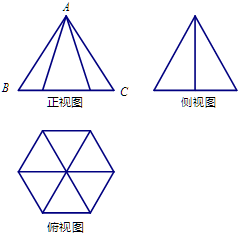
A.12 B.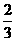
C.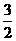 D.6
D.6
答案 C
8.(2009枣庄一模)一个几何体的三视图如右图所示,则该几何体外接球的表面积为 ( )
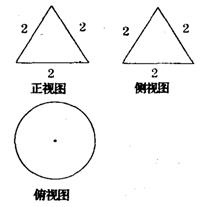 A.
A.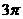 B.
B. [来源:高&考%资(源#网]
[来源:高&考%资(源#网]
C.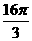 D.以上都不对
D.以上都不对
答案C
7. (2009泰安一模)一个几何体的三视图如图所示,则这个几何体的
(2009泰安一模)一个几何体的三视图如图所示,则这个几何体的
体积等于
(A) 4 (B) 6
(C) 8 (D)12
答案A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com