
题目列表(包括答案和解析)
1、(2009青岛一模)已知点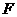 、
、 分别为双曲线
分别为双曲线 :
: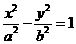
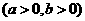 的左焦点、右顶点,点
的左焦点、右顶点,点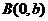 满足
满足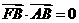 ,则双曲线的离心率为
,则双曲线的离心率为
A. B.
B.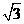 C.
C. 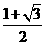 D.
D.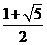
答案 D
8.(池州市七校元旦调研)在 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为 、
、 、
、 ,已知
,已知 ,且
,且 求b
求b
分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1) 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)
左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)  过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解法一:在 中
中 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有: 化简并整理得:
化简并整理得: .又由已知
.又由已知
 .解得
.解得 .
.
解法二:由余弦定理得: 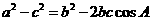 .又
.又 ,
,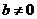 。
。
所以 …………………………………①
…………………………………①
又 ,
,
 ,即
,即
由正弦定理得 ,故
,故 ………………………②
………………………②
由①,②解得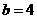 。
。
7. (肥城市第二次联考)(本小题满分12分)
(肥城市第二次联考)(本小题满分12分)
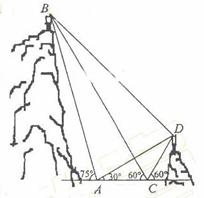
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为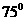 ,
,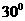 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
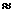 1.414,
1.414,
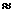 2.449)
2.449)
解:
在△ABC中,∠DAC=30°, ∠ADC=60°-∠DAC=30,
所以CD=AC=0.1 又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA, ……5分
在△ABC中,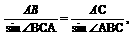
即AB=
因此,BD=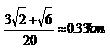
故B,D的距离约为0.33km。 ……12分
6.(哈师大附中、东北师大附中、辽宁省实验中学)
设 的内角
的内角 所对的边分别为
所对的边分别为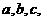 且
且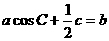 .
.
(1)求角 的大小;
的大小;
(2)若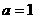 ,求
,求 的周长
的周长 的取值范围.
的取值范围.
解:(1)由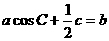 得
得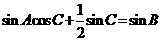 …………
…………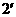
又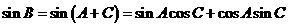 …………
…………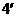
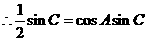 ,
,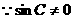 ,
,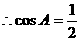 ,
,
又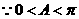
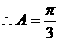 …………
…………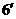
(2)由正弦定理得: ,
,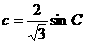
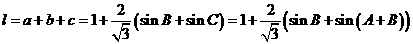 ………
………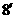
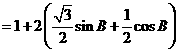
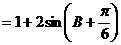 …………
…………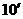
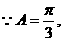
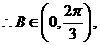
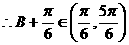
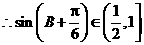
故 的周长
的周长 的取值范围为
的取值范围为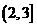 .
…………
.
…………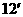
(2)另解:周长
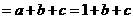 由(1)及余弦定理
由(1)及余弦定理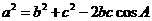
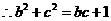 …………
…………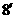

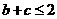 …………
…………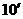
又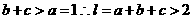
即 的周长
的周长 的取值范围为
的取值范围为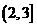 .
…………
.
…………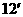
5.(哈师大附中、东北师大附中、辽宁省实验中学)
(1)由“若 则
则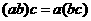 ”类比“若
”类比“若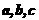 为三个向量则
为三个向量则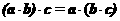 ”
”
(2)在数列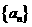 中,
中,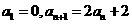 猜想
猜想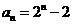
(3)在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”
(4)已知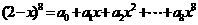 ,则
,则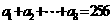 .
.
上述四个推理中,得出的结论正确的是____ .(写出所有正确结论的序号)
答案(2)(3)
4. 的三内角A,B,C所对边长分别是
的三内角A,B,C所对边长分别是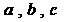 ,设向量
,设向量
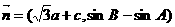 ,若
,若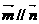 ,则角
,则角 的大小为_____________
的大小为_____________
答案 
3. (祥云一中三次月考理)已知边长为1的正三角形 中,则
中,则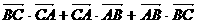 的值为
的值为
A.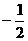 B.
B.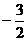 C.
C.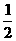 D.
D. 
答案:B
2.设点 在
在 内部,且
内部,且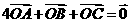 ,则
,则 的面积与
的面积与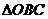 的面积之比是
的面积之比是
A.2:1 B.3:1 C.4:3 D.3:2
答案:D
1.(马鞍山学业水平测试)△AOB是边长为1的等边三角形,O是原点,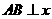 轴,以O为顶点,且过A,B的抛物线的方程是
轴,以O为顶点,且过A,B的抛物线的方程是
A. B.
B.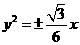 C.
C.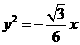 D.
D. 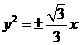
答案 B
2010年联考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com