
题目列表(包括答案和解析)
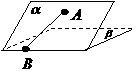
4.(2010四川文)(15)如图,二面角 的大小是60°,线段
的大小是60°,线段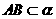 .
.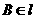 ,
,
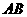 与
与 所成的角为30°.则
所成的角为30°.则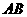 与平面
与平面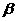 所成的角的正弦值是
.
所成的角的正弦值是
.
[答案]
[解析]过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,故∠ADC为二面角 的平面角,为60°
的平面角,为60°
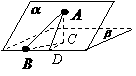 又由已知,∠ABD=30°连结CB,则∠ABC为
又由已知,∠ABD=30°连结CB,则∠ABC为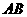 与平面
与平面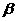 所成的角
所成的角
设AD=2,则AC=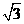 ,CD=1
,CD=1
AB=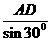 =4
=4
∴sin∠ABC=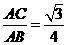
3.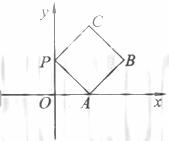 (2010北京理)(14)如图放置的边长为1的正方形PABC沿x轴滚动。设顶点p(x,y)的轨迹方程是
(2010北京理)(14)如图放置的边长为1的正方形PABC沿x轴滚动。设顶点p(x,y)的轨迹方程是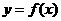 ,则
,则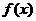 的最小正周期为
;
的最小正周期为
;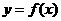 在其两个相邻零点间的图像与x轴所围区域的面积为
在其两个相邻零点间的图像与x轴所围区域的面积为
[答案]4 
说明:“正方形PABC沿 轴滚动”包括沿
轴滚动”包括沿 轴正方向和沿
轴正方向和沿 轴负方向滚动。沿
轴负方向滚动。沿 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿 轴负方向滚动。
轴负方向滚动。
2.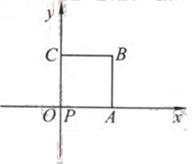 (2010北京文)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京文)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的纵坐标与横坐标的函数关系是
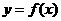 ,则
,则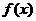 的最小正周期为
;
的最小正周期为
;
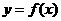 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
[答案]4 
说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
1.(2010江西理)16.如图,在三棱锥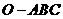 中,三条棱
中,三条棱 ,
, ,
, 两两垂直,且
两两垂直,且 >
> >
> ,分别经过三条棱
,分别经过三条棱 ,
, ,
, 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为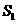 ,
,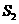 ,
,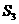 ,则
,则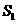 ,
,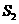 ,
,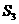 的大小关系为
。
的大小关系为
。
[答案] 
[解析]考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得 。
。
8.(2010四川文)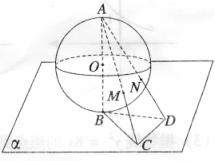 (12)半径为
(12)半径为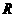 的球
的球 的直径
的直径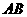 垂直于平面
垂直于平面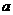 ,垂足为
,垂足为 ,
,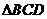 是平面
是平面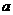 内边长为
内边长为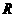 的正三角形,线段
的正三角形,线段 、
、 分别与球面交于点
分别与球面交于点 、
、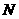 ,那么
,那么 、
、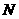 两点间的球面距离是
两点间的球面距离是
(A) (B)
(B)
(C)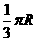 (D)
(D)
[答案]A
[解析]由已知,AB=2R,BC=R,故tan∠BAC=
cos∠BAC=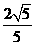
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=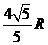 ,同理AN=
,同理AN=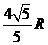 ,且MN∥CD
,且MN∥CD
而AC=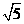 R,CD=R
R,CD=R
故MN:CD=AN:AC
Þ MN= ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=
所以M、N两点间的球面距离是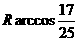
7.(2010全国卷1理)(7)正方体ABCD- 中,B
中,B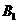 与平面AC
与平面AC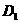 所成角的余弦值为
所成角的余弦值为
(A) 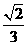 (B)
(B)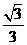 (C)
(C)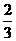 (D)
(D)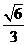

6.(2010全国卷1理)(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A)  (B)
(B)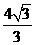 (C)
(C)  (D)
(D) 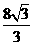

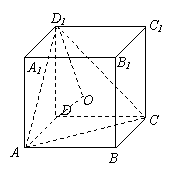
5.(2010全国卷1文)(9)正方体 -
- 中,
中, 与平面
与平面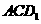 所成角的余弦值为
所成角的余弦值为
(A) 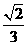 (B)
(B)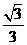 (C)
(C)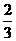 (D)
(D)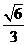
 [答案]D
[答案]D
[命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC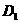 的距离是解决本题的关键所在,这也是转化思想的具体体现.
的距离是解决本题的关键所在,这也是转化思想的具体体现.
[解析1]因为BB1//DD1,所以B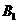 与平面AC
与平面AC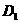 所成角和DD1与平面AC
所成角和DD1与平面AC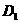 所成角相等,设DO⊥平面AC
所成角相等,设DO⊥平面AC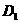 ,由等体积法得
,由等体积法得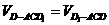 ,即
,即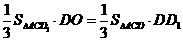 .设DD1=a,
.设DD1=a,
则 ,
, .
.
所以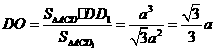 ,记DD1与平面AC
,记DD1与平面AC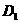 所成角为
所成角为 ,则
,则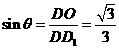 ,所以
,所以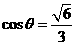 .
.
[解析2]设上下底面的中心分别为 ;
;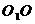 与平面AC
与平面AC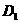 所成角就是B
所成角就是B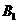 与平面AC
与平面AC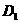 所成角,
所成角,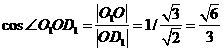
4.(2010全国卷2文)(8)已知三棱锥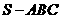 中,底面
中,底面 为边长等于2的等边三角形,
为边长等于2的等边三角形,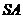 垂直于底面
垂直于底面 ,
,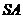 =3,那么直线
=3,那么直线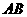 与平面
与平面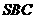 所成角的正弦值为
所成角的正弦值为
(A)
 (B)
(B)

(C)
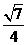 (D)
(D) 
[答案]D
[解析]:本题考查了立体几何的线与面、面与面位置关系及直线与平面所成角。
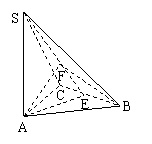 过A作AE垂直于BC交BC于E,连结SE,过A作AF垂直于SE交SE于F,连BF,∵正三角形ABC,∴ E为BC中点,∵ BC⊥AE,SA⊥BC,∴ BC⊥面SAE,∴ BC⊥AF,AF⊥SE,∴ AF⊥面SBC,∵∠ABF为直线AB与面SBC所成角,由正三角形边长3,∴
过A作AE垂直于BC交BC于E,连结SE,过A作AF垂直于SE交SE于F,连BF,∵正三角形ABC,∴ E为BC中点,∵ BC⊥AE,SA⊥BC,∴ BC⊥面SAE,∴ BC⊥AF,AF⊥SE,∴ AF⊥面SBC,∵∠ABF为直线AB与面SBC所成角,由正三角形边长3,∴
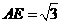 ,AS=3,∴ SE=
,AS=3,∴ SE= ,AF=
,AF= ,∴
,∴

3.(2010全国卷2文)(11)与正方体ABCD-A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个
[答案]D
[解析]:本题考查了空间想象能力
∵到三条两垂直的直线距离相等的点在以三条直线为轴,以正方体边长为半径的圆柱面上,∴三个圆柱面有无数个交点,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com