
题目列表(包括答案和解析)
2.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________。
[解析]设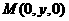 由
由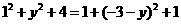 可得
可得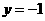 故
故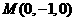
[答案](0,-1,0)
1.若等边 的边长为
的边长为 ,平面内一点
,平面内一点 满足
满足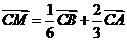 ,则
,则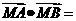 _________
_________
13.(2010江苏卷)16、(本小题满分14分)
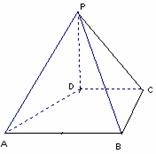 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
[解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查几何体的体积,考查空间想象能力、推理论证能力和运算能力。满分14分。
(1)证明:因为PD⊥平面ABCD,BC 平面ABCD,所以PD⊥BC。
平面ABCD,所以PD⊥BC。
由∠BCD=900,得CD⊥BC,
又PD DC=D,PD、DC
DC=D,PD、DC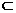 平面PCD,
平面PCD,
所以BC⊥平面PCD。
因为PC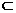 平面PCD,故PC⊥BC。
平面PCD,故PC⊥BC。
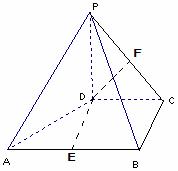 (2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=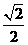 ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于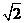 。
。
(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得 的面积
的面积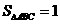 。
。
由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积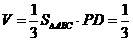 。
。
因为PD⊥平面ABCD,DC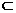 平面ABCD,所以PD⊥DC。
平面ABCD,所以PD⊥DC。
又PD=DC=1,所以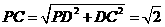 。
。
由PC⊥BC,BC=1,得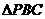 的面积
的面积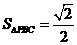 。
。
由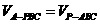 ,
,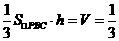 ,得
,得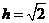 ,
,
故点A到平面PBC的距离等于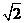 。
。
2009年高考题
12.(2010湖南理)


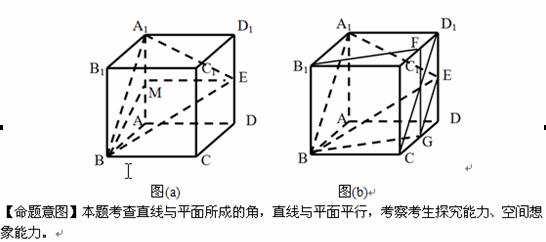
11.(2010福建文)20. (本小题满分12分)
如图,在长方体ABCD – A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH//A1D1。过EH的平面与棱BB1,CC1相交,交点分别为F,G。
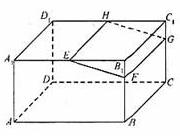 (I)证明:AD//平面EFGH;
(I)证明:AD//平面EFGH;
(II)设AB=2AA1=2a。在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE – D1DCGH内的概率为p。当点E,F分别在棱A1B1, B1B上运动且满足EF=a时,求p的最小值。


10.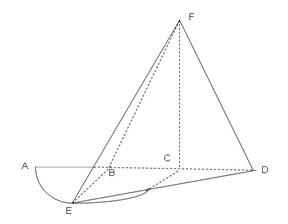 (2010广东文)18.(本小题满分14分)
(2010广东文)18.(本小题满分14分)
如图4,弧AEC是半径为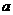 的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC
的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC 平面BED,FB=
平面BED,FB=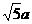
(1)证明:EB FD
FD
(2)求点B到平面FED的距离.
(1)证明: 点E为弧AC的中点
点E为弧AC的中点

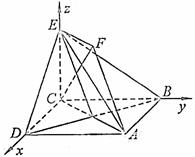
9.(2010北京理)(16)(本小题共14分)
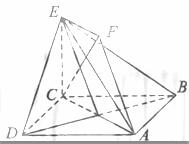 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=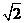 ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小。
证明:(I) 设AC与BD交与点G。
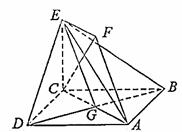 因为EF//AG,且EF=1,AG=
因为EF//AG,且EF=1,AG= AC=1.
AC=1.
所以四边形AGEF为平行四边形.
所以AF//平面EG,
因为 平面BDE,AF
平面BDE,AF 平面BDE,
平面BDE,
所以AF//平面BDE.
(II)因为正方形ABCD和四边形ACEF所在的平面
相互垂直,且CE AC,
AC,
所以CE 平面ABCD.
平面ABCD.
如图,以C为原点,建立空间直角坐标系C- .
.
 则C(0,0,0),A(
则C(0,0,0),A(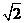 ,
,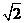 ,0),B(0,
,0),B(0,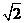 ,0).
,0).
所以 ,
,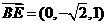 ,
,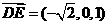 .
.
所以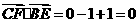 ,
,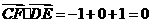
所以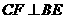 ,
,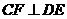 .
.
所以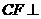 BDE.
BDE.
(III) 由(II)知, 是平面BDE的一个法向量.
是平面BDE的一个法向量.
设平面ABE的法向量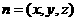 ,则
,则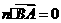 ,
,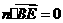 .
.
即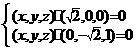
所以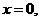 且
且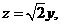
令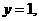 则
则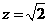 .
.
所以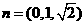 .
.
从而 。
。
因为二面角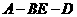 为锐角,
为锐角,
所以二面角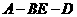 的大小为
的大小为 .
.
8.(2010北京文)(18) (本小题共14分)
设定函数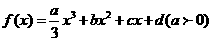 ,且方程
,且方程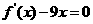 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当a=3且曲线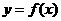 过原点时,求
过原点时,求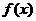 的解析式;
的解析式;
(Ⅱ)若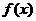 在
在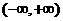 无极值点,求a的取值范围。
无极值点,求a的取值范围。
解:由 得
得 
因为 的两个根分别为1,4,所以
的两个根分别为1,4,所以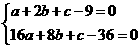 (*)
(*)
(Ⅰ)当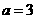 时,又由(*)式得
时,又由(*)式得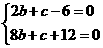
解得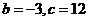
又因为曲线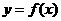 过原点,所以
过原点,所以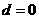
故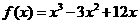
(Ⅱ)由于a>0,所以“ 在(-∞,+∞)内无极值点”等价于“
在(-∞,+∞)内无极值点”等价于“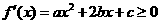 在(-∞,+∞)内恒成立”。
在(-∞,+∞)内恒成立”。
由(*)式得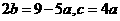 。
。
又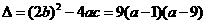
解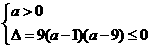 得
得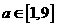
即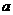 的取值范围
的取值范围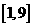
7.(2010重庆理)(19)(本小题满分12分,(I)小问5分,(II)小问7分)
如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,PA 底面ABCD,PA=AB=
底面ABCD,PA=AB=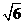 ,点E是棱PB的中点。
,点E是棱PB的中点。
(I) 求直线AD与平面PBC的距离;
(II)
若AD=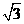 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。





6.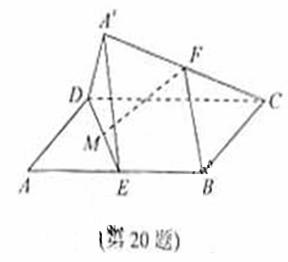 (2010浙江文)(20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(2010浙江文)(20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com