
题目列表(包括答案和解析)
14.(祥云一中三次月考文)(本小题满分12分)
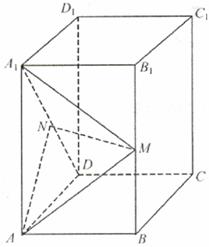 如图,已知正四棱柱
如图,已知正四棱柱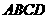 -
-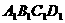 中AB=1,A
中AB=1,A =2,N是
=2,N是 D的中点,点M在BB
D的中点,点M在BB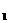 上,异面直线MN、
上,异面直线MN、 A互相垂直.
A互相垂直.
(1)试确定点M的位置,并加以证明;
(2)求二面角A-MN- 的大小.
的大小.
解:(Ⅰ)取A1A的中点P,连PM、PN,则PN//AD,
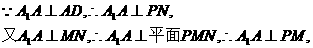

(Ⅱ)由(Ⅰ)知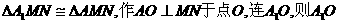 ,
,
则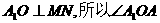 就是所求二面角的平面角.
就是所求二面角的平面角.
显然
利用等面积法求得A1O=AO=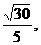 在△A1OA中由余弦定理得
在△A1OA中由余弦定理得
cos∠A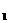 OA=
OA=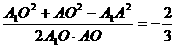
所以二面角的大小为

解二:(向量法) (咯)
13. 解:以CD为x轴,CA为y轴,以CE为z轴建立空间坐标系,
(1)C(0,0,0),D(1,0,0),A(0,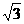 ,0),F(0,
,0),F(0,
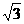 ,
,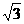 ),B(-1,
),B(-1,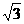 ,0),
,0),

12.(祥云一中三次月考理)(本小题满分12分)
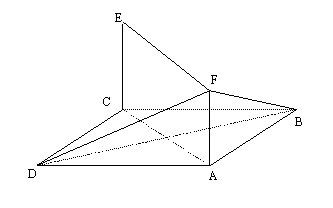
如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,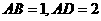 ,
,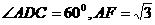 .
.
(1)求证:AC⊥BF;
(2)求二面角F-BD-A的大小.

11. (祥云一中二次月考理)(本小题满分12分)
(祥云一中二次月考理)(本小题满分12分)
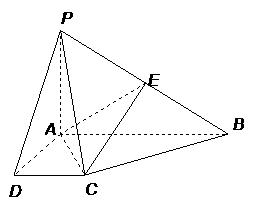
如图所示,四棱锥P-ABCD中,侧棱PA与底面ABCD垂直,DC=1,AD=AP=2,AB=5,∠CDA=∠DAB=90°,E是PB的中点.
(1)求证:BC⊥平面PAC;
(2)求异面直线PD、AE所成角的大小;
(3)求二面角A-CE-B的大小..
法一: (1)证:由题意:AC=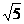 ,则
,则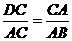 ,又∠DCA=∠CAB,所以△DCA 与△CAB
相似,所以 BC⊥AC,又由侧棱PA与底面ABCD垂直,有PA ⊥BC,
,又∠DCA=∠CAB,所以△DCA 与△CAB
相似,所以 BC⊥AC,又由侧棱PA与底面ABCD垂直,有PA ⊥BC,
所以BC⊥平面PAC;……………4分
(2)连BD,取BD的中点M,连EM,
则EM‖PD,△AEM中,AE=AM= ,EM=
,EM= ,设异面直线PD、AE所成角为
,设异面直线PD、AE所成角为 ,则
,则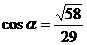 ,所以PD、AE所成角为
,所以PD、AE所成角为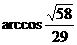 .
.
(3)作AH⊥PC于H,作HK⊥EC于K,连AK,又(1)可知.∠AKH即为所求二面角的平面角的补角.在△APC中求出AH=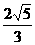 ,在△ACE中求出AK=
,在△ACE中求出AK=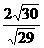 ,(或在△PCE中求出HK=
,(或在△PCE中求出HK=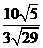 )
)
所求二面角的大小为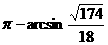 (或为
(或为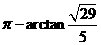 ).
).
法二:(坐标法)(2)PD、AE所成角为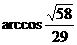 .
.
(3)所求二面角的大小为: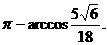
10.解:
 如图取DC的中点O,连PO,∵△PDC为正三角形,∴PO⊥DC.
如图取DC的中点O,连PO,∵△PDC为正三角形,∴PO⊥DC.
又∵面PDC⊥面ABCD,∴PO⊥面ABCD.如图建立空间直角坐标系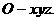
则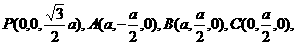
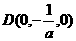
(1)E为PC中点,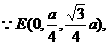
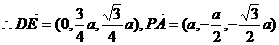 ,
,
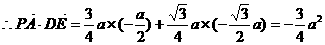 ,
,
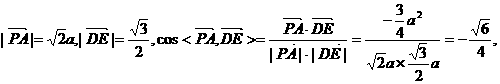
………………………………….6分
(2)可求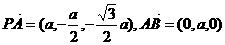 ,
,
设面PAB的一个法向量为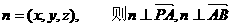 ,
,
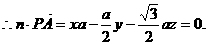 ①
① 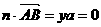 .
②
.
②
由②得y=0,代入①得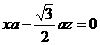 令
令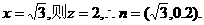
则D到面PAB的距离d等于
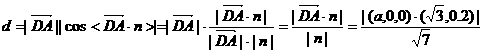
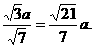 即点D到面PAB的距离等于
即点D到面PAB的距离等于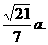 ……………………………..12分
……………………………..12分
9.(祥云一中月考理)(本小题满分12分)
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点。
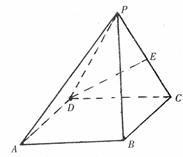 (I)求异面直线PA与DE所成的角的余弦值;
(I)求异面直线PA与DE所成的角的余弦值;
(II)求点D到面PAB的距离.
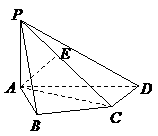
8. (玉溪一中期中文)(本小题12分)如图,在四棱锥 中,
中,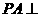 底面
底面 ,
,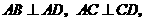
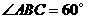 ,
,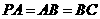 ,
, 是
是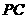 的中点.
的中点.
(Ⅰ)求 和平面
和平面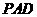 所成的角的大小;
所成的角的大小;
 (Ⅱ)证明
(Ⅱ)证明 平面
平面 ;
;
(Ⅲ)求二面角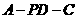 的大小.
的大小.
(Ⅰ)解:在四棱锥 中,因
中,因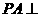 底面
底面 ,
,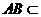 平面
平面 ,故
,故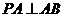 .
.
又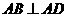 ,
,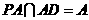 ,从而
,从而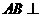 平面
平面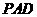 .故
.故 在平面
在平面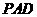 内的射影为
内的射影为 ,从而
,从而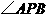 为
为 和平面
和平面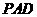 所成的角.
所成的角.
 在
在 中,
中, ,故
,故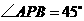 .
.
所以 和平面
和平面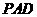 所成的角的大小为
所成的角的大小为 .
.
(Ⅱ)证明:在四棱锥 中,
中,
因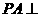 底面
底面 ,
,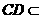 平面
平面 ,故
,故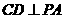 .
.
由条件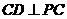 ,
, ,
,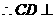 面
面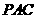 .
.
又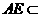 面
面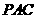 ,
,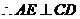 .
.
由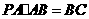 ,
,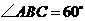 ,可得
,可得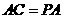 .
.
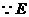 是
是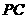 的中点,
的中点,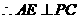 ,
, .综上得
.综上得 平面
平面 .
.
(Ⅲ)解:过点 作
作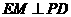 ,垂足为
,垂足为 ,连结
,连结 .由(Ⅱ)知,
.由(Ⅱ)知, 平面
平面 ,
, 在平面
在平面 内的射影是
内的射影是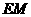 ,则
,则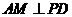 .
.
因此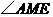 是二面角
是二面角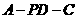 的平面角.
的平面角.
由已知,可得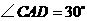 .设
.设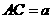 ,可得
,可得
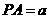 ,
,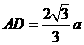 ,
, ,
,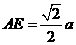 .
.
在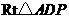 中,
中,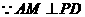 ,∴
,∴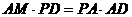 ,则
,则
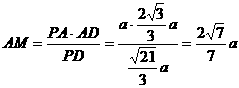 .
.
在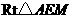 中,
中, .所以二面角
.所以二面角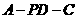 的大小
的大小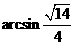
7.(马鞍山学业水平测试)(本小题满分12分)
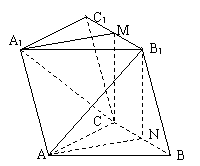
 (文)在斜三棱柱
(文)在斜三棱柱 中,M为
中,M为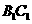 的中点,N是BC上一点.
的中点,N是BC上一点.
(Ⅰ)若平面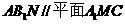 ,求证:N为BC的中点;
,求证:N为BC的中点;
(Ⅱ)在(Ⅰ)的条件下,若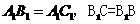 ,求证:
,求证: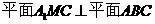 .
.
 (Ⅰ)
(Ⅰ)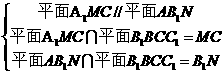 ,所以
,所以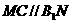
因为M为B1C1中点,所以N为BC中点----------------------6分
(Ⅱ)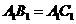 ,且M为中点,所以
,且M为中点,所以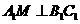 ----------8分
----------8分
 ,M为中点,所以
,M为中点,所以 ,----------10分
,----------10分
又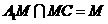 ,则
,则 ,
----------12分
,
----------12分
又 ,所以
,所以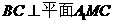 ,
----------14分
,
----------14分
又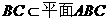 ,所以
,所以
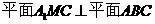 -------16分
-------16分
5. (马鞍山学业水平测试)(本小题满分8分)
(马鞍山学业水平测试)(本小题满分8分)
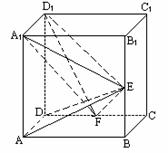
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(Ⅰ)证明:AD⊥D1F;
(Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明:面AED⊥面A1FD1.
解:以D为原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系.
设正方体的棱长为1…………………………………………………………………………1分
则有A(1,0,0),E(1,2, ),F(0,
),F(0, ,0),D1(0,0,1),A1(1,0,1)……2分
,0),D1(0,0,1),A1(1,0,1)……2分
(Ⅰ)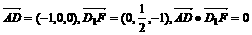 ,∴AD⊥D1F………………………4分
,∴AD⊥D1F………………………4分
(Ⅱ)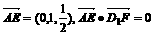 ,∴AE⊥D1F
,∴AE⊥D1F
AE与D1F所成的角为900…………………………………………………………………6分
(Ⅲ)由以上可知D1F⊥平面AED,又D1F在平面A1FD1内,
∴面AED⊥面A1FD1……………………………………………………………………8分
|
 平面
平面 ,
,
 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为 ,
,
 ,
, 的中点,
的中点, ,
,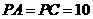 .
.
(I)设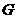 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(II)证明:在 内存在一点
内存在一点 ,使
,使 平面
平面 .
.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在
直线为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O ,则
,则

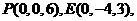
 ,由题意得,
,由题意得,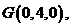 因
因 ,因此平面BOE的法向量为
,因此平面BOE的法向量为 ,
, 得
得 ,又直线
,又直线 不在平面
不在平面 内,因此有
内,因此有 平面
平面
(II)设点M的坐标为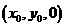 ,则
,则 ,因为
,因为 平面BOE,所以有
平面BOE,所以有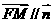 ,因此有
,因此有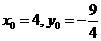 ,即点M的坐标为
,即点M的坐标为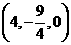 ,在平面直角坐标系
,在平面直角坐标系 中,
中, 的内部区域满足不等式组
的内部区域满足不等式组 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在 内存在一点
内存在一点 ,使
,使 平面
平面 ,
,
4.(池州市七校元旦调研)设向量 ,
,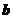 满足:
满足: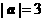 ,
,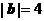 ,
,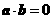 .以
.以 ,
,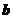 ,
,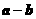 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为 的圆的公共点个数最多为 ( )
的圆的公共点个数最多为 ( )
A.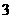 B.
B.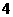 C.
C.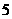 D.
D.
答案:C
[解析]对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com